如图15所示，发射人造卫星时，先把卫星送入近地点Q，然后使其沿椭圆轨道到达远地点P，此时速度为v.若P点到地心的距离为R，卫星的总质量为m，地球半径为R0，地表的重力加速度为g，则欲使卫星从P点起绕地球做半径为R的圆轨道运动，卫星在P点处应将质量为Δm的燃气以多大的对地速度向后喷出？（将连续喷气等效为一次性喷气）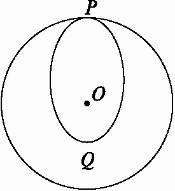
图15
如图所示，一个质量是2千克的木块A夹在完全相同的甲、乙两个固定的木板间，木板甲、乙对木块A的压力都为20牛，用力F沿竖直方向向上拉木块A，当力F=44牛时，物体A匀速向上运动，求木块与木板间的动摩擦因数等于多少，若用竖直向下的力
将木块向下匀速拉出，所加力大小为多少？（g=10m/s
）
甲、乙两个同学在跑道上练习4×100m接力，他们在奔跑时有相同的最大速度。乙从静止开始全力奔跑需跑25m才能达到最大速度，这一过程可看作匀加速运动。现在甲持棒以最大速度向已奔来，乙在接力区待机全力奔出。若要求乙接棒时奔跑速度达到最大速度的80%，则（1）乙在接力区须奔出多少距离？（2）乙应在距离甲多远时起跑？
汤姆生在测定阴极射线荷质比时采用的方法是利用电场、磁场偏转法。即测出阴极射线在匀强电场或匀强磁场中穿过一定距离时的偏角。设匀强电场的电场强度为E，阴极射线垂直电场射入、穿过水平距离L后的运动偏角为θ（θ较小，θ≈tanθ）（如图8-15A）；以匀强磁场B代替电场，测出经过同样长的一段弧长L的运动偏角为φ（如图8-15B），试以E、B、L、θ、φ表示组成阴极射线粒子荷质比q/m的关系式（重力不计）
如图所示，A是一块水平放置得铅板的截面，其厚度为d。MM´和NN´是一重力可忽略不计，质量为m，带电量为q的粒子在匀强磁场中的运动轨迹。粒子的运动轨迹与磁场方向垂直，并且粒子垂直穿过铅板。轨迹MM´的半径为r，轨迹NN´的半径为R，且R > r。求：
（1）粒子穿过铅板时的运动方向（回答向上或向下）
（2）粒子带何电荷。
（3）粒子穿过铅板时所受的平均阻力。
粤公网安备 44130202000953号