如图16-4-14所示,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、βm(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为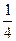 R,碰撞中无机械能损失.重力加速度为g.试求:
R,碰撞中无机械能损失.重力加速度为g.试求:
图16-4-14
(1)待定系数β;
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.
如图16-4-14所示,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、βm(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为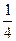 R,碰撞中无机械能损失.重力加速度为g.试求:
R,碰撞中无机械能损失.重力加速度为g.试求:
图16-4-14
(1)待定系数β;
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.