一直流电压表，量程为1 ，内阻为1 ，现将一阻值为5000~之间的固定电阻与此电压表串联，以扩大电压表的量程。为求得扩大后量程的准确值，再给定一直流电源（电动势为6~7 ，内阻可忽略不计），一阻值=的固定电阻，两个单刀开关及若干线.。
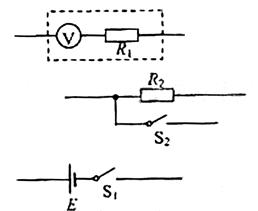
（1）为达到上述目的，将答题卡上对应的图连成一个完整的实验电路图。
（2）连线完成以后，当与均闭合时，电压表的示数为0.90 ；当闭合，断开时，电压表的示数为0.70 ，由此可以计算出改装后电压表的量程为V，电源电动势为
如图，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点。一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=2m处由静止开始沿轨道向右运动，力作用一段距离后撤去，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合。规定经过O点水平向右为x轴正方向。小车与轨道间的动摩擦因数μ=0.2，g取10m/s2。
（1）若小球刚好落到A点，求小车运动到O′点的速度；
（2）为使小球刚好落在A点，圆盘转动的角速度应为多大？
（3）为使小球能落到圆盘上，求水平拉力F作用的距离范围。
已知地球到太阳的距离约为1.5×1011m，万有引力常量为G=6.67×10-11N、m2/kg2。试由常识通过计算求：
（1）太阳的质量M（保留一位有效数字）;
（2）已知火星绕太阳做圆周运动的周期为1.9地球年，求地球与火星相邻两次距离最近时的时间间隔t。
把一个质量为0.5kg的小球，以20m/s的初速度竖直向上抛出，运动过程中小球始终受到水平方向大小恒为F=10N的风力的作用，g=10m/s2,求:
（1) 小球上升的最大高度H。
（2）小球在空中滞留的时间。
（3）小球落地点与抛出点之间的水平距离（设地面水平）。
如图所示装置中，区域I和Ⅲ中分别有竖直向上和水平向右的匀强电场，电场强度分别为E和
；Ⅱ区域内有垂直纸面向外的水平匀强磁场，磁感应强度为B。一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度V0水平射人电场，经水平分界线OP上的A点与OP成600角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的匀强电场中。求：
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径
(2)O、M间的距离
(3)粒子从M点出发到第二次通过CD边界所经历的时间
粤公网安备 44130202000953号