如图所示,在光滑水平面上有一条柔软的质量为m、长为L的均匀链条,开始时,这个链条有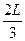 长在桌面上,而
长在桌面上,而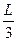 长垂于桌外.若不计能量损失,求:
长垂于桌外.若不计能量损失,求: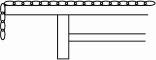
(1)把它的悬垂部分拉回到桌面,至少做多少功?
(2)如果让它由静止开始下滑,当全部链条离开桌面时,这条链条的速率是多大?
如图所示,在光滑水平面上有一条柔软的质量为m、长为L的均匀链条,开始时,这个链条有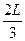 长在桌面上,而
长在桌面上,而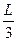 长垂于桌外.若不计能量损失,求:
长垂于桌外.若不计能量损失,求:
(1)把它的悬垂部分拉回到桌面,至少做多少功?
(2)如果让它由静止开始下滑,当全部链条离开桌面时,这条链条的速率是多大?