下图是用一个逻辑电路、电键S、安装在室外的光敏电阻R0、定值电阻R1和滑动变阻器R2组成的报警系统控制电路。该控制系统的功能是:工作日的晚上(光线较暗),报警系统自动开始工作;非工作日只要合上电键S,报警系统24小时都能工作(报警系统工作时,逻辑电路输出端为高电位)。
在两个虚线框内分别画上光敏电阻或定值电阻,并在实线框内标上门电路的符号,该门电路 是________门电路。
是________门电路。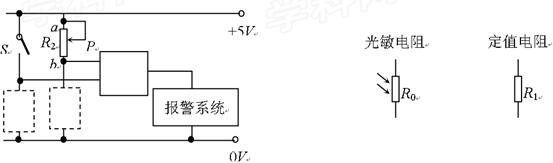
下图是用一个逻辑电路、电键S、安装在室外的光敏电阻R0、定值电阻R1和滑动变阻器R2组成的报警系统控制电路。该控制系统的功能是:工作日的晚上(光线较暗),报警系统自动开始工作;非工作日只要合上电键S,报警系统24小时都能工作(报警系统工作时,逻辑电路输出端为高电位)。
在两个虚线框内分别画上光敏电阻或定值电阻,并在实线框内标上门电路的符号,该门电路 是________门电路。
是________门电路。