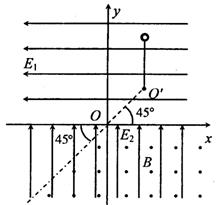
如图所示,在x轴上方有水平向左的匀强电场,电场强度为E1;下方有竖直向上的匀强电场,电场强度为E2,且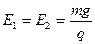 。在x轴下方的虚线(虚线与茗轴成45°角)右侧有垂直纸面向外的匀强磁场,磁感应强度为B。有一长为L的轻绳一端固定在第一象限内的O′点,且可绕O′点在竖直平面内转动;另一端拴有一质量为m的小球,小球带电量为+q。OO′与x轴成45°角,其长度也为L。先将小球放在O′点正上方,从绳恰好绷直处由静止释放,小球刚进人有磁场的区域时将绳子断开。
。在x轴下方的虚线(虚线与茗轴成45°角)右侧有垂直纸面向外的匀强磁场,磁感应强度为B。有一长为L的轻绳一端固定在第一象限内的O′点,且可绕O′点在竖直平面内转动;另一端拴有一质量为m的小球,小球带电量为+q。OO′与x轴成45°角,其长度也为L。先将小球放在O′点正上方,从绳恰好绷直处由静止释放,小球刚进人有磁场的区域时将绳子断开。
试求:
(1)绳子第一次刚拉直还没有开始绷紧时小球的速度大小;
(2)小球刚进入有磁场的区域时的速度大小;
(3)小球从进入有磁场的区域到第一次打在x轴上经过的时间。