如图,质量为M=1kg的平板车左端放有一质量为m=2kg的铁块,铁块与车之间的动摩擦因数u=0.5。开始时车和铁块以速度 =6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求
=6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求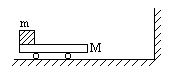
(1)铁块相对于车的总路程。
(2)小车和墙第一次相碰后所走的总路程。
如图,质量为M=1kg的平板车左端放有一质量为m=2kg的铁块,铁块与车之间的动摩擦因数u=0.5。开始时车和铁块以速度 =6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求
=6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求
(1)铁块相对于车的总路程。
(2)小车和墙第一次相碰后所走的总路程。