如图所示,N=100匝的正方形线N,边长L=10cm,电阻r=1Ω.在匀强磁场中,B=0.4T,以n=100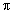 r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
(1)从中性面开始计时,写出线圈中产生电动势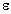 的表达式;
的表达式;
(2)电压表的示数;
(3)当线圈和中性面夹角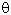 =
=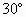 ,安培力的力矩 M安=?
,安培力的力矩 M安=?
(4)1min内,外力所做的功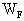 =?
=?
如图所示,N=100匝的正方形线N,边长L=10cm,电阻r=1Ω.在匀强磁场中,B=0.4T,以n=100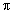 r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
(1)从中性面开始计时,写出线圈中产生电动势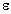 的表达式;
的表达式;
(2)电压表的示数;
(3)当线圈和中性面夹角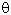 =
=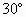 ,安培力的力矩 M安=?
,安培力的力矩 M安=?
(4)1min内,外力所做的功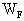 =?
=?