如图所示,一矩形线圈面积为400 、匝数为100匝,绕线圈的中心轴
、匝数为100匝,绕线圈的中心轴 以角速度
以角速度 匀速转动,匀强磁场磁感强度为
匀速转动,匀强磁场磁感强度为 T,转动轴与磁感线垂直。线圈电阻为1Ω,
T,转动轴与磁感线垂直。线圈电阻为1Ω, =3Ω,
=3Ω,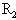 =6Ω,
=6Ω, =12Ω,其余电阻不计,电键S断开。当线圈转到线圈平面与磁感线平行时,所受磁场力的力矩为16N·m,求:
=12Ω,其余电阻不计,电键S断开。当线圈转到线圈平面与磁感线平行时,所受磁场力的力矩为16N·m,求:
(1)线圈转动的角速度ω。
(2)感应电动势的最大值。
(3)电键S闭合后,线圈的输出功率。
如图所示,一矩形线圈面积为400 、匝数为100匝,绕线圈的中心轴
、匝数为100匝,绕线圈的中心轴 以角速度
以角速度 匀速转动,匀强磁场磁感强度为
匀速转动,匀强磁场磁感强度为 T,转动轴与磁感线垂直。线圈电阻为1Ω,
T,转动轴与磁感线垂直。线圈电阻为1Ω, =3Ω,
=3Ω,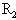 =6Ω,
=6Ω, =12Ω,其余电阻不计,电键S断开。当线圈转到线圈平面与磁感线平行时,所受磁场力的力矩为16N·m,求:
=12Ω,其余电阻不计,电键S断开。当线圈转到线圈平面与磁感线平行时,所受磁场力的力矩为16N·m,求:
(1)线圈转动的角速度ω。
(2)感应电动势的最大值。
(3)电键S闭合后,线圈的输出功率。