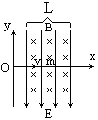如图所示，在宽为L=8cm的空间区域里，存在着互相垂直的匀强电场和匀强磁场，电场方向竖直向下，磁场方向垂直xy平面，x方向垂直二场的边界，y方向平行边界，一束不计重力的带电粒子以速度V，沿x轴进入这一区域，恰好不改变运动方向，作匀速直线运动．若粒子以V射入时，只有电场，测得粒子穿过这一区域后，在y方向偏移了3.2cm．若粒子以原速原路射入时，只有磁场，则粒子穿过这一区域后，在y方向偏移了多少?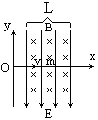
相关试题
如图所示，放在长木板上的木块质量为m，当木板与水平方向夹角为α时，木块静止在长木板上。
（1）求此时木块所受的弹力和摩擦力各多大？
（2）当把木块的倾角增大到θ（θ>α）时，木块刚好沿长木板匀速下滑，求木块和木板之间的动摩擦因数为多大？
.一半径为R的光滑圆环固定在竖直平面内，环上套两个中央有孔的小球A和B，A、B间由质量不计的原长为R的细弹簧连接着，它们处于如图中的位置时恰好都能保持静止状态，此时B球与环中心O处于同一水平面上，AB与水平线成30°夹角。已知B球的质量为m，求A球的质量和弹簧的劲度系数。
粤公网安备 44130202000953号