如图是建筑工地常用的一种“深坑打夯机”，电动机带动两个滚轮匀速转动将夯杆从深坑提上来，当夯杆底端刚到达坑口时，两个滚轮彼此分开，将夯杆释放，夯杆在重力作用下落回深坑。夯实坑底。已知两个滚轮边缘的线速度恒为v=4m/s，滚轮对夯杆的压力FN=2×104N，滚轮与夯杆间的动摩擦因数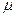
=0.3，夯杆质量m=1×103kg，坑深h=6.4m，取g=10m/s2，求：
（1）夯杆自坑底开始匀加速上升，当速度增加到4m/s时，夯杆上升的高度；
（2）夯杆自坑底上升的最大高度；
相关试题
如图是建筑工地常用的一种“深坑打夯机”，电动机带动两个滚轮匀速转动将夯杆从深坑提上来，当夯杆底端刚到达坑口时，两个滚轮彼此分开，将夯杆释放，夯杆在重力作用下落回深坑。夯实坑底。已知两个滚轮边缘的线速度恒为v=4m/s，滚轮对夯杆的压力FN=2×104N，滚轮与夯杆间的动摩擦因数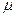=0.3，夯杆质量m=1×103kg，坑深h=6.4m，取g=10m/s2，求：
（1）夯杆自坑底开始匀加速上升，当速度增加到4m/s时，夯杆上升的高度；
（2）夯杆自坑底上升的最大高度；
粤公网安备 44130202000953号