有一个长方形小木盒ABCD,质量为180g.木盒高L=0.2m,其顶部离挡板M的竖直距离h=0.8m.在木盒内放有一个20g的小物体P(可视为质点).通过细绳对静止木盒施加一个竖直向上的恒定拉力F.为了使木盒能向上运动,并且当木盒AD和挡板M相碰时木盒停止运动后,P物体不会和木盒顶部AD相碰.求拉力F的大小范围.(空气阻力不计,取g=10m/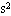 )
)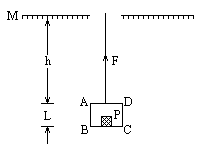
有一个长方形小木盒ABCD,质量为180g.木盒高L=0.2m,其顶部离挡板M的竖直距离h=0.8m.在木盒内放有一个20g的小物体P(可视为质点).通过细绳对静止木盒施加一个竖直向上的恒定拉力F.为了使木盒能向上运动,并且当木盒AD和挡板M相碰时木盒停止运动后,P物体不会和木盒顶部AD相碰.求拉力F的大小范围.(空气阻力不计,取g=10m/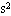 )
)