天文工作者观测到某行星的半径为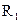 ,自转周期为
,自转周期为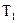 ,它有一颗卫星,轨道半径为
,它有一颗卫星,轨道半径为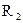 ,绕行星公转周期为
,绕行星公转周期为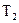 .若万有引力常量为
.若万有引力常量为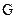 .求:
.求:
(1)该行星的平均密度;
(2)要在此行星的赤道上发射一颗质量为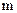 的近地人造卫星,使其轨道沿赤道上方,且设行星上无气体阻力,则对卫星至少应做多少功?
的近地人造卫星,使其轨道沿赤道上方,且设行星上无气体阻力,则对卫星至少应做多少功?
天文工作者观测到某行星的半径为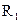 ,自转周期为
,自转周期为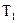 ,它有一颗卫星,轨道半径为
,它有一颗卫星,轨道半径为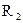 ,绕行星公转周期为
,绕行星公转周期为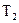 .若万有引力常量为
.若万有引力常量为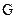 .求:
.求:
(1)该行星的平均密度;
(2)要在此行星的赤道上发射一颗质量为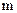 的近地人造卫星,使其轨道沿赤道上方,且设行星上无气体阻力,则对卫星至少应做多少功?
的近地人造卫星,使其轨道沿赤道上方,且设行星上无气体阻力,则对卫星至少应做多少功?