如图所示,有一柔软链条全长为L=1.0 m,质量均匀分布,总质量为M=2.0kg.整条链条均匀带电,总带电量 ,将链条放在离地足够高的水平桌面上.仅在水平桌面的上方存在匀强电场,电场强度
,将链条放在离地足够高的水平桌面上.仅在水平桌面的上方存在匀强电场,电场强度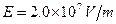 .若桌面与链条之间的动摩擦因数为
.若桌面与链条之间的动摩擦因数为 (重力加速度取g=10m/s2).试求:
(重力加速度取g=10m/s2).试求:
(1)当桌面下的链条多长时,桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力。
(2)链条从桌面上全部滑下所需的最小初动能。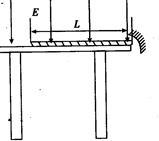
如图所示,有一柔软链条全长为L=1.0 m,质量均匀分布,总质量为M=2.0kg.整条链条均匀带电,总带电量 ,将链条放在离地足够高的水平桌面上.仅在水平桌面的上方存在匀强电场,电场强度
,将链条放在离地足够高的水平桌面上.仅在水平桌面的上方存在匀强电场,电场强度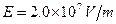 .若桌面与链条之间的动摩擦因数为
.若桌面与链条之间的动摩擦因数为 (重力加速度取g=10m/s2).试求:
(重力加速度取g=10m/s2).试求:
(1)当桌面下的链条多长时,桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力。
(2)链条从桌面上全部滑下所需的最小初动能。