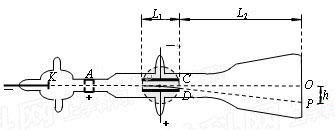
1897年汤姆生通过对阴极射线的研究,发现了电子,从而使人们认识到原子是可分的。汤姆生当年用来测定电子比荷(电荷量e与质量m之比)的实验装置如图所示,真空玻璃管内 C、D为平行板电容器的两极,圆形阴影区域内可由管外电磁铁产生一垂直纸面的匀强磁场,圆形区域的圆心位于C、D中心线的中点,直径与C、D的长度相等。已知极板C、D的长度为L1,C、D间的距离为d,极板右端到荧光屏的距离为L2。由K发出的电子,经A与K之间的高电压加速后,形成一束很细的电子流,电子流沿C、D中心线进入板间区域。
C、D为平行板电容器的两极,圆形阴影区域内可由管外电磁铁产生一垂直纸面的匀强磁场,圆形区域的圆心位于C、D中心线的中点,直径与C、D的长度相等。已知极板C、D的长度为L1,C、D间的距离为d,极板右端到荧光屏的距离为L2。由K发出的电子,经A与K之间的高电压加速后,形成一束很细的电子流,电子流沿C、D中心线进入板间区域。
若C、D间无电压,则电子将打在荧光屏上的O点;若在C、D间加上电压U,则电子将打在荧光屏上的P点,P点到O点的距离为h;若再在圆形区域内加一方向垂直于纸面向外、磁感应强度为B的匀强磁场,则电子又打在荧光屏上的O点。不计重力影响。
(1)求电子打在荧光屏O点时速度的大小。
(2)推导出电子比荷的表达式。
(3)利用这个装置,还可以采取什么方法测量电子的比荷?
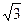 ,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.
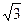 ,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.