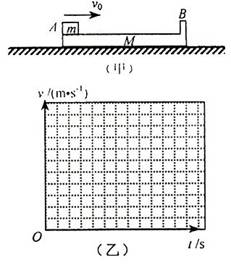
如图（甲）所示，质量为M、长L=1.0m、右端带有竖直挡板的木板B，静止在光滑水平面上.质量为m的小木块（可视为质点）A，以水平速度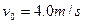
滑上B的左端，在右端与B碰撞后，最后恰好滑回木板B的左端. 已知
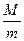=3，并且在A与挡板碰撞时无机械能损失，忽略碰撞时间，取g=10m/s2，求：
（1）木块A与木板B间的动摩擦因数；
（2）在图（乙）所给坐标系中，画出此过程中B对地的速度——时间图线.
相关试题
如图（甲）所示，质量为M、长L=1.0m、右端带有竖直挡板的木板B，静止在光滑水平面上.质量为m的小木块（可视为质点）A，以水平速度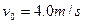滑上B的左端，在右端与B碰撞后，最后恰好滑回木板B的左端. 已知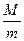=3，并且在A与挡板碰撞时无机械能损失，忽略碰撞时间，取g=10m/s2，求：
（1）木块A与木板B间的动摩擦因数；
（2）在图（乙）所给坐标系中，画出此过程中B对地的速度——时间图线.
粤公网安备 44130202000953号