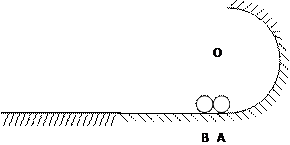粗糙水平地面与光滑半圆形轨道连接，两个小球A、B可视为质点，最初A、B两球静止在半圆形轨道圆心O的正下方，如图所示。若A、B球之间夹有一小块炸药，炸药爆炸后，小球A恰能经过半圆形轨道的最高点，B球到达的最远位置恰好是A球在水平地面上的落点；已知粗糙水平地面与B球之间的摩擦因数为0.2，求A、B两球的质量之比。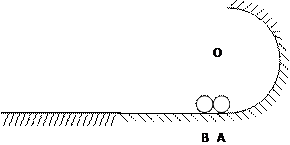
相关试题
紫光在真空中的波长为
，红光在真空中波长为
，玻璃对紫光的折射率为1.54，对红光的折射率为1.5．
（1）紫光、红光的频率各是多少?
（2）紫光、红光在玻璃中传播的波长各是多少?
资料一：驾驶员的反应时间：0.3s~0.6s之间
资料二：各种路面与轮胎之间的动摩擦因数：
| 路面 |
动摩擦因数 |
| 干沥青与混凝土路面 |
0.7—0.8 |
| 干碎石路面 |
0.6—0.7 |
| 湿沥青与混凝土路面 |
0.32—0.4 |
（1）在计算中驾驶员的反应时间应该取多少？为什么？
（2）在计算中路面与轮胎之间的动摩擦因数应该取多少？为什么？
（3）通过你的计算来说明多少米为必要的安全距离。
（1）为使粒子始终在半径为R的圆轨道上运动，磁场必须周期性递增。求粒子从t=0时刻起绕行第n圈时的磁感应强度
；
（2）求粒子从t=0时刻起绕行n圈回到P板所需的总时间
。
，A球被竖直下抛，B球和C球分别被沿着彼此相反的水平方向抛出。若空气阻力不计，重力加速度取
，求：
粤公网安备 44130202000953号