如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为 ,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们的质量和电阻分别为
,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们的质量和电阻分别为 和
和 ,两杆与导轨接触良好,与导轨间的动摩擦因数为
,两杆与导轨接触良好,与导轨间的动摩擦因数为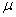 ,已知:杆1被外力拖动,以恒定的速度
,已知:杆1被外力拖动,以恒定的速度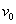 沿导轨运动;达到稳定状态时,杆2也以恒定速度沿导轨运动,导轨的电阻可忽略,求此时杆2克服摩擦力做功的功率。
沿导轨运动;达到稳定状态时,杆2也以恒定速度沿导轨运动,导轨的电阻可忽略,求此时杆2克服摩擦力做功的功率。
如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为 ,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们的质量和电阻分别为
,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们的质量和电阻分别为 和
和 ,两杆与导轨接触良好,与导轨间的动摩擦因数为
,两杆与导轨接触良好,与导轨间的动摩擦因数为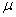 ,已知:杆1被外力拖动,以恒定的速度
,已知:杆1被外力拖动,以恒定的速度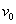 沿导轨运动;达到稳定状态时,杆2也以恒定速度沿导轨运动,导轨的电阻可忽略,求此时杆2克服摩擦力做功的功率。
沿导轨运动;达到稳定状态时,杆2也以恒定速度沿导轨运动,导轨的电阻可忽略,求此时杆2克服摩擦力做功的功率。