某宇航员在太空站内做了如下实验:选取两个质量分别为mA=0.1kg、mB=0.2kg的小球A、B和一根轻质短弹簧,弹簧的一端与小球A粘连,另一端与小球B接触而不粘连.现使小球A和B之间夹着被压缩的轻质弹簧,处于锁定状态,一起以速度v0=0.1m/s做匀速直线运动,如图所示.过一段时间,突然解除锁定(解除锁定没有机械能损失),两球仍沿原直线运动,从弹簧与小球B刚刚分离开始计时,经时间t=3.0s,两球之间的距离增加了s=2.7m,求弹簧被锁定时的弹性势能Ep?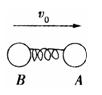
某宇航员在太空站内做了如下实验:选取两个质量分别为mA=0.1kg、mB=0.2kg的小球A、B和一根轻质短弹簧,弹簧的一端与小球A粘连,另一端与小球B接触而不粘连.现使小球A和B之间夹着被压缩的轻质弹簧,处于锁定状态,一起以速度v0=0.1m/s做匀速直线运动,如图所示.过一段时间,突然解除锁定(解除锁定没有机械能损失),两球仍沿原直线运动,从弹簧与小球B刚刚分离开始计时,经时间t=3.0s,两球之间的距离增加了s=2.7m,求弹簧被锁定时的弹性势能Ep?