如图11-12所示，由电容器和磁场组成一射线管，电容器极板长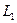
＝5cm，两板间距d＝5cm，两端加电压U＝10V，电容器右侧有一宽度为
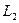＝5cm弱磁场区域，其磁感应强度B＝
T，方向竖直向下，在磁场边界的右边s＝10m处，放置一个标有坐标的屏，现有初速度
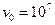m/s的负离子束从电容器中心水平向右入射（荷质比g＝
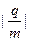＝5×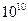
C/kg）．若不加电压和磁场时，离子束恰打在坐标的原点上，那么加上电压和磁场后离子束应打在坐标纸上的哪个位置?（结果精确到0.1cm）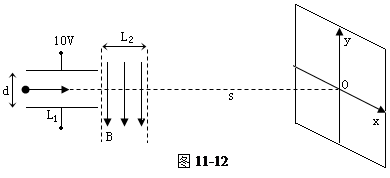
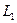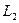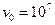如图11-12所示，由电容器和磁场组成一射线管，电容器极板长＝5cm，两板间距d＝5cm，两端加电压U＝10V，电容器右侧有一宽度为＝5cm弱磁场区域，其磁感应强度B＝T，方向竖直向下，在磁场边界的右边s＝10m处，放置一个标有坐标的屏，现有初速度m/s的负离子束从电容器中心水平向右入射（荷质比g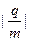＝＝5×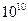C/kg）．若不加电压和磁场时，离子束恰打在坐标的原点上，那么加上电压和磁场后离子束应打在坐标纸上的哪个位置?（结果精确到0.1cm）
粤公网安备 44130202000953号