有足够长的平行金属导轨,电阻不计,导轨光滑,间距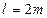 .现将导轨沿与水平方向成
.现将导轨沿与水平方向成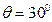 角倾斜放置.在底部接有一个
角倾斜放置.在底部接有一个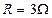 的电阻.现将一个长为
的电阻.现将一个长为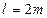 、质量
、质量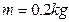 、电阻
、电阻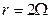 的金属棒自轨道顶部沿轨道自由滑下,经一段距离后进入一垂直轨道平面的匀强磁场中(如图12-17所示).磁场上部有边界,下部无边界,磁感应强度
的金属棒自轨道顶部沿轨道自由滑下,经一段距离后进入一垂直轨道平面的匀强磁场中(如图12-17所示).磁场上部有边界,下部无边界,磁感应强度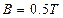 .金属棒进入磁场后又运动了
.金属棒进入磁场后又运动了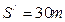 后开始做匀速直线运动,在做匀速直线运动之前这段时间内电阻R上产生了
后开始做匀速直线运动,在做匀速直线运动之前这段时间内电阻R上产生了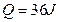 的内能(
的内能( ).求:
).求: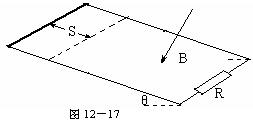
(1)金属棒进入磁场后速度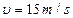 时的加速度a的大小及方向;
时的加速度a的大小及方向;
(2)磁场的上部边界距顶部的距离S.
有足够长的平行金属导轨,电阻不计,导轨光滑,间距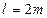 .现将导轨沿与水平方向成
.现将导轨沿与水平方向成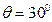 角倾斜放置.在底部接有一个
角倾斜放置.在底部接有一个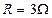 的电阻.现将一个长为
的电阻.现将一个长为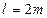 、质量
、质量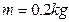 、电阻
、电阻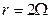 的金属棒自轨道顶部沿轨道自由滑下,经一段距离后进入一垂直轨道平面的匀强磁场中(如图12-17所示).磁场上部有边界,下部无边界,磁感应强度
的金属棒自轨道顶部沿轨道自由滑下,经一段距离后进入一垂直轨道平面的匀强磁场中(如图12-17所示).磁场上部有边界,下部无边界,磁感应强度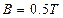 .金属棒进入磁场后又运动了
.金属棒进入磁场后又运动了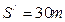 后开始做匀速直线运动,在做匀速直线运动之前这段时间内电阻R上产生了
后开始做匀速直线运动,在做匀速直线运动之前这段时间内电阻R上产生了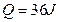 的内能(
的内能( ).求:
).求:
(1)金属棒进入磁场后速度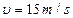 时的加速度a的大小及方向;
时的加速度a的大小及方向;
(2)磁场的上部边界距顶部的距离S.