如图13-1所示，物体A从高h的P处沿光滑曲面从静止开始下滑，物体B用长为L的细绳竖直悬挂在O点且刚和平面上Q点接触。已知mA=mB，高h及S(平面部分长)。若A和B碰撞时无能量损失。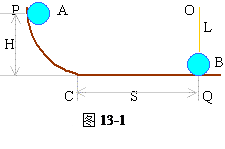
(1)若L≤h/4，碰后A、B各将做什么运动?
(2)若L=h，且A与平面的动摩擦因数为μ，A、B可能碰撞几次？A最终在何处？
如图所示，物体A的质量为1kg，物体B的质量为2kg，物体A与物体B之间的动摩擦因数为0.2，物体B与水平桌面之间的动摩擦因数为0.3．若不计细绳及滑轮的质量，也不计细绳与滑轮之间的摩擦，要使物体B被水平细绳从物体A下部抽出来，物体C质量应为多大?（g取10m/
）
质量为m＝2.0kg的小铁块静止于水平导轨AB的A端．导轨及支架ABCD的形状如图，其重心在图中的O点，质量M＝4.0kg，可绕通过支架D点的垂直于纸面的水平轴自由转动，现加一个沿导轨方向的恒力F，通过细线作用于铁块，F＝12N，铁块和导轨之间的动摩擦因数μ＝0.50，重力加速度g＝10m／
．从加力的时刻算起，导轨（及支架）能保持静止的最长时间是多少?
在运动的升降机中天花板上用细线悬挂一个物体Ａ，下面吊着一个轻质弹簧秤（弹簧秤的质量不计），弹簧秤下吊着物体Ｂ，如图所示。物体Ａ和Ｂ的质量相等，都为m＝5kg，某一时刻弹簧秤的读数为40 N，设ｇ＝10m/s2。
求细线的拉力。
若将细线剪断，求在剪断细线瞬间物体Ａ和B的加速度的大小和方向。
均匀木板AB长L＝1.6m，质量M＝2kg，如图所示，转轴0距地面高度h＝0.6m，木板AO部分长L＝1m．有一滑块质量m＝1kg，以初速度V0＝8m/s沿木板上滑．滑块与木板间动摩擦因数μ＝0.5，g取10m/
求：
(1)滑块滑到什么位置时，木板开始翻动?
(2)翻转时滑块的速度多大?
(3)滑块从起始时刻到木板翻转时刻用的时间?
km，试求在赤道上空相对于地球静止的同步卫星距地面的高度h，并求同步卫星发射回地球的信号可覆盖的范围(以对地心的圆心角表示)．
粤公网安备 44130202000953号