如图3-12-30所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A 、B .它们的质量分别为mA、mB,弹簧的劲度系数为k , C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A 使之向上运动,求物块B 刚要离开C时物块A 的加速度a 和从开始到此时物块A 的位移d,重力加速度为g.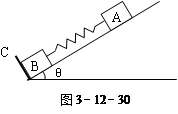
如图3-12-30所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A 、B .它们的质量分别为mA、mB,弹簧的劲度系数为k , C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A 使之向上运动,求物块B 刚要离开C时物块A 的加速度a 和从开始到此时物块A 的位移d,重力加速度为g.