广东省深圳市石岩公学八年级3月质量检测数学试卷
下列说法中正确的是( )
A. 是 是 的一个解 的一个解 |
B. 是 是 的解集 的解集 |
C. 是 是 的唯一解 的唯一解 |
D. 不是 不是 的解 的解 |
若不等式(a-3)x>a-3的解集是x<1,则a的取值范围是( )
A.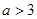 |
B.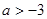 |
C.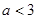 |
D. |
到三角形三个顶点的距离相等的点是三角形( )的交点.
| A.三个内角平分线 | B.三边垂直平分线 | C.三条中线 | D.三条高 |
已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是( )
| A.7㎝ | B.9㎝ | C.12㎝ | D.12㎝或者9㎝ |
对“等角对等边”这句话的理解,正确的是 ( )
| A.只要两个角相等,那么它们所对的边也相等 |
| B.在两个三角形中,如果有两个角相等,那么它们所对的边也相等 |
| C.在一个三角形中,如果有两个角相等,那么它们所对的边也相等 |
| D.以上说法都是错误的 |
一个等腰三角形的一个内角是40°,则它的顶角是( )
| A.40° | B.50° | C.60° | D.40° ,100° |
如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( )
| A.30° | B.36° | C.45° | D.70° |
如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1 B.2 C.3 D.4
某校男子100m跑的记录是12s,在今年的校田径运动会上,肖华的100m跑成绩是ts,打破了该校男子100m跑的记录。上述数量关系可用不等式表示为___________
如图,BD是∠ABC的平分线,P是BD上的一点,PE⊥BA于点E,PE=4㎝,则点P到边BC的距离是 cm
解不等式:(1) 8x+1<6x-3 (2)解不等式:5x-9<3(x+1)
(3) (4)
(4)
如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.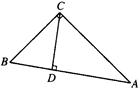
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
如图,已知:D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE.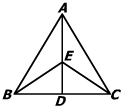
证明:在△AEB和△AEC中,
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程;
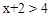 的解表示在数轴上,正确的是( )
的解表示在数轴上,正确的是( )
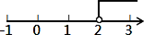
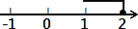

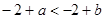
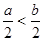





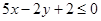
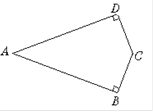
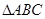 中
中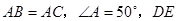 是腰
是腰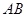 的垂直平分线,
的垂直平分线,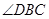 的度数是 。
的度数是 。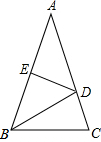
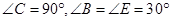 .
.

 ,△AEC的面积为
,△AEC的面积为 。则
。则 边上的高,请你证明小明的猜想。
边上的高,请你证明小明的猜想。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号