山东省泰安市泰山区九年级上学期期末学情检测数学试卷
已知⊙O1和⊙O2的半径分别是2cm和6cm,且O1O2=8cm,则这两圆的位置关系是
| A.内切 | B.相交 | C.外离 | D.外切 |
若⊙O的直径为20cm,点O到直线l的距离为10cm,则直线l与⊙O的位置关系是
| A.相交 | B.相切 | C.相离 | D.无法确定 |
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长是
| A.4cm | B.6cm | C.8cm | D.10cm |
将抛物线 向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为
向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为
A. |
B. |
C. |
D. |
如图,在⊙O中,弦AB∥CD,若∠ABC=36°,则∠BOD等于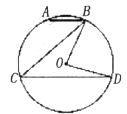
| A.18° | B.36° | C.54° | D.72° |
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间的关系满足
A. |
B. |
C. |
D. |
在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定
| A.与x轴相切,与y轴相切 | B.与x轴相切,与y轴相交 |
| C.与x轴相交,与y轴相切 | D.与x轴相交,与y轴相交 |
如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为
A.  B.
B.  C.
C.  D.
D. 
如图,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为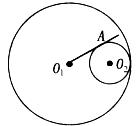
| A.2 | B.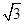 |
C.4 | D. |
如图,P是⊙O外一点,PA、PB切⊙O于点A、B,Q是优弧AB上的一点,设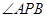 =
=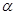 ,∠AQB=
,∠AQB=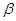 ,则
,则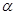 与
与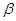 的关系是
的关系是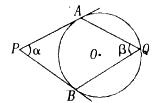
A. 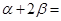 90° B.
90° B. 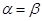 C.
C. 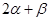 =180° D.
=180° D. 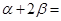 180°
180°
在半径为1的⊙O中,弦AB的长为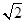 ,则弦AB所对的圆周角的度数为
,则弦AB所对的圆周角的度数为
| A.45° | B.60° | C.45°或135° | D.60°或120° |
如图,AB切⊙O于点B,OA=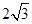 ,∠A=30°,弦BC∥OA,则劣弧
,∠A=30°,弦BC∥OA,则劣弧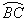 的弧长为
的弧长为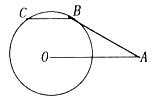
A.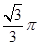 |
B. |
C.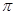 |
D.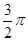 |
如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为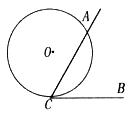
| A.4 | B.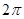 |
C.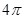 |
D. |
如图,以点P为圆心,以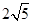 为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为
为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为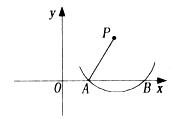
A.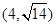 |
B.(4,2) | C.(4,4) | D.(2,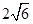 ) ) |
如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为
A. |
B. |
C. |
D. |
用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是_______。
如图,两圆相交于A、B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为_______。
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于E,BD交CE于点F,
的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长。
某宾馆有30个房间供游客住宿,当每个房间的房价为每天160元时,房间会全部住满。当每个房间每天的房价每增加10元时,就会有一个房间空闲。宾馆需对游客居住的每个房间每天支出20元的各种费用。根据规定,每个房间每天的房价不得高于260元。
设每个房间的房价每天增加x元(x为10的整数倍)。
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P。
(1)求证:AP是⊙O的切线;
(2)若OC=CP,AB= ,求CD的长。
,求CD的长。
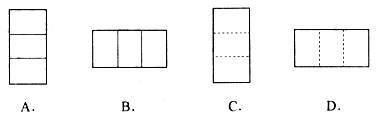
 ,则
,则 的值等于
的值等于



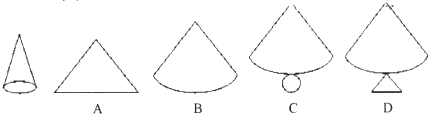
 的图象大致是下图的
的图象大致是下图的
 与底面半径r的关系是
与底面半径r的关系是



 的图象与x轴只有一个公共点,则常数m的值是_______
的图象与x轴只有一个公共点,则常数m的值是_______
 粤公网安备 44130202000953号
粤公网安备 44130202000953号