[湖北]2014届湖北省大冶市九年级上学期期末考试数学试卷
若x1,x2是一元二次方程x2﹣3x+2=0的两根,则x1+x2的值是( )
| A.﹣2 | B.2 | C.3 | D.1 |
用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
| A.(x+2)2=1 | B.(x﹣2)2=1 | C.(x+2)2=9 | D.(x﹣2)2=9 |
抛物线y=x2﹣2x+3的顶点坐标是( )
| A.(1,﹣2) | B.(1,2) | C.(﹣1,2) | D.(﹣1,﹣2) |
“抛一枚均匀硬币,落地后正面朝上”这一事件是( )
| A.必然事件 | B.随机事件 | C.确定事件 | D.不可能事件 |
若两圆的半径分别是2cm和5cm,圆心距为3cm,则这两圆的位置关系是( )
| A.外离 | B.相交 | C.外切 | D.内切 |
如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于( )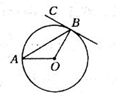
A.15° B.20° C.30° D.70°
已知二次函数y=a(x+1)2﹣b(a≠0)有最小值1,则a,b的大小关系为( )
| A.a>b | B.a<b | C.a=b | D.不能确定 |
已知关于x的一元二次方程x2﹣2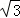 x+k=0有两个不相等的实数根,则k的取值范围是 _________ .
x+k=0有两个不相等的实数根,则k的取值范围是 _________ .
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 _________ .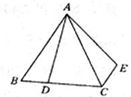
如图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则∠AFB= _________ °.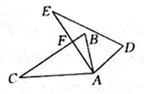
一个不透明的布袋中分别标着数字1,2,3,4的四个乒乓球,先从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于4的概率为 _________ .
已知抛物线y=k(x+1)(x﹣ )与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是 _________ .
)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是 _________ .
甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛,求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
如图1,已知点D在A上,△ABC和△ADE都是等腰直角三角形,点M为BC的中点
(1)求证:△BMD为等腰直角三角形.
(2)将△ADE绕点A逆时针旋转45°,如图2中的“△BMD为等腰直角三角形”是否仍然成立?请说明理由.
(3)将△ADE绕点A任意旋转一定的角度,如图3中的“△BMD为等腰直角三角形”是否均成立?说明理由.




 ﹣1=( )
﹣1=( )
 有意义,则x的取值范围是 _________ .
有意义,则x的取值范围是 _________ . ﹣
﹣ ×
× ﹣(2﹣
﹣(2﹣ )2.
)2.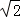 x﹣4=0.
x﹣4=0.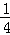 mn=0有两个相等的正实数根,求
mn=0有两个相等的正实数根,求 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号