2013年初中数学单元提优测试卷-点的坐标与待定系数法求函数
点(﹣1,y1),(2,y2),(3,y3)均在函数 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
点A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数 的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A.y3<y1<y2 | B.y1<y2<y3 |
| C.y3<y2<y1 | D.y2<y1<y3 |
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
| A.1 | B.﹣5 | C.4 | D.1或﹣5 |
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y= (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
A.1<k<2 B.1≤k≤3 C.1≤k≤4 D.1≤k<4
已知:多项式x2﹣kx+1是一个完全平方式,则反比例函数y= 的解析式为( )
的解析式为( )
A.y= |
B.y=﹣ |
C.y= 或y=﹣ 或y=﹣ |
D.y= 或y=﹣ 或y=﹣ |
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 的图象上.若点A的坐标为(﹣2,﹣2),则k的值为( )
的图象上.若点A的坐标为(﹣2,﹣2),则k的值为( )
| A.1 | B.﹣3 | C.4 | D.1或﹣3 |
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y= (x>0)的图象上,顶点A1、B1分别在x轴和y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴和y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y= (x>0)的图象上,顶点A2在x轴的正半轴上,则P2点的坐标为 _________ ,P3的坐标为 _________ .
(x>0)的图象上,顶点A2在x轴的正半轴上,则P2点的坐标为 _________ ,P3的坐标为 _________ .
两个反比例函数 的图象在第一象限,第二象限如图,点P1、P2、P3…P2010在
的图象在第一象限,第二象限如图,点P1、P2、P3…P2010在 的图象上,它们的横坐标分别是有这样规律的一行数列1,3,5,7,9,11,…,过点P1、P2、P3、…、P2010分别作x轴的平行线,与
的图象上,它们的横坐标分别是有这样规律的一行数列1,3,5,7,9,11,…,过点P1、P2、P3、…、P2010分别作x轴的平行线,与 的图象交点依次是Q1、Q2、Q3、…、Q2010,则点Q2010的横坐标是 .
的图象交点依次是Q1、Q2、Q3、…、Q2010,则点Q2010的横坐标是 .
若点(﹣2,y1)、(﹣1,y2)、(1,y3)都在反比例函数 的图象上,则用“>”连接y1、y2、y3得 .
的图象上,则用“>”连接y1、y2、y3得 .
已知反比例函数 的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1﹣y2 0(填写“<”或“>”).
的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1﹣y2 0(填写“<”或“>”).
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 恰好经过点E,AB=4,AD=2,则K的值是 .
恰好经过点E,AB=4,AD=2,则K的值是 .
已知点P(﹣1,n)在双曲线y= 上.
上.
(1)若点P(﹣1,n)在直线y=﹣3x上,求m的值;
(2)若点P(﹣1,n)在第三象限,点A(x1,y1),B(x2,y2)在双曲线 上,且
上,且 ,试比较y1,y2的大小.
,试比较y1,y2的大小.
两个反比例函数 ,
, 在第一象限内的图象,如图,点P1,P2,P3,…,P2005在反比例函数
在第一象限内的图象,如图,点P1,P2,P3,…,P2005在反比例函数 图象上,它们的横坐标分别为x1,x2,x3,…,x2005,纵坐标分别为1,3,5,…,共2005个连续奇数,过点P1,P2,P3,…,P2005分别作y轴的平行线,与
图象上,它们的横坐标分别为x1,x2,x3,…,x2005,纵坐标分别为1,3,5,…,共2005个连续奇数,过点P1,P2,P3,…,P2005分别作y轴的平行线,与 的图象交点,依次是Q1(x1,y1),Q1(x2,y2),Q1(x3,y3),…,Q1(x2005,y2005),求y2005的值.
的图象交点,依次是Q1(x1,y1),Q1(x2,y2),Q1(x3,y3),…,Q1(x2005,y2005),求y2005的值.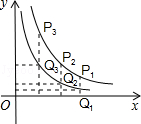
已知函数y=y1﹣y2,且y1为x的反比例函数,y2为x的正比例函数,且 和x=1时,y的值都是1.求y关于x的函数关系式.
和x=1时,y的值都是1.求y关于x的函数关系式.
已知变量y与2x成反比例,且当x=2时,y=6,
(1)求y与x之间的函数关系.
(2)请判断点B(3,4)是否在这个反比例函数的图象上,并说明理由.
已知y=y1﹣y2,且y1与x的算术平方根成正比例,y2与x的平方成反比例,当x=1时,y=0;x=2时,y= ,求y关于x的表达式.
,求y关于x的表达式.
如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数  (k为常数,k≠0)的图象相交于点 A(1,3).
(k为常数,k≠0)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点B的坐标;
(2)点C(a,b)在反比例函数  的图象上,求当1≤a≤3时,b的取值范围;
的图象上,求当1≤a≤3时,b的取值范围;
(3)观察图象,写出使函数值y1≥y2的自变量x的取值范围.
 ,若x1<x2,其对应值y1,y2的大小关系是
,若x1<x2,其对应值y1,y2的大小关系是  在第一象限内的点,求
在第一象限内的点,求 的值.
的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号