[江苏]2011-2012学年江苏苏州星港学校七年级第二学期5月月考数学试卷
下列各组条件中,能判定△ABC≌△DEF的是 ( )
| A.AB=DE,BC=EF,∠A=∠D |
| B.∠A=∠D,∠C=∠F,AC=EF |
| C.AB=DE,BC=EF,△ABC的周长= △DEF的周长 |
| D.∠A=∠D,∠B=∠E,∠C=∠F |
下列各组图形中,一定全等的是 ( )
| A.两个等边三角形 |
| B.腰长相等的两个等腰三角形 |
| C.两边和一角对应相等的两个三角形 |
| D.两边对应相等的两个直角三角形 |
如图,AB=AD,添加下面的一个条件后.仍无法判定△ABC≌△ADC的是 ( )
| A.CB=CD | B.∠BAC=∠DAC |
| C.∠BCA=∠DCA | D.∠B=∠D=90° |
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是 ( )
| A.3 | B.4 | C.5 | D.6 |

解方程组 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么 ( )
那么 ( )
| A.a、b、c的值不能确定 | B.a=4,b=5,c=-2 |
| C.a、b不能确定,c=-2 | D.a=4,b=7,c=2 |
如图,已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有几个( )
(1)AD平分∠EDF;(2)△EBD≌△FCD;(3)BD=CD;(4)AD⊥BC.
A.1个 B.2个 C.3个 D.4个 
一宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团20人准备同时租用这三种客房共7间.若每个房间都住满,则租房的方案有 ( )
| A.4种 | B.3种 | C.2种 | D.1种 |
如图,△ABC中,∠C=90°,AC=BD ,AD平分∠CAB交BC于D,DE⊥AB,垂足为点E,AB=12㎝,DC=5cm,则△DEB的周长为 .
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
如图,点C为线段AB上一点,△ACM和△CBN是等边三角形,若BM="5" cm,则AN= .
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE 平分∠ADC,∠CED=35°,如图,则∠EAB是 .
三个同学对问题:“若方程组 的解是
的解是 求方程组
求方程组 的解”提出了各自的想法.甲说:“这个题目好像条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“能不能把第二个方程组中两个方程的两边都除以5,通过换元的方法来解决.”参考他们的讨论,你认为这个题目的解是 .
的解”提出了各自的想法.甲说:“这个题目好像条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“能不能把第二个方程组中两个方程的两边都除以5,通过换元的方法来解决.”参考他们的讨论,你认为这个题目的解是 .
如图,点C、E、B、F在同一直线上,AC//DF,AC="DF,BF=CE," △ABC与△DEF全等吗?说明你的理由.
如图,AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于点F.
试说明F是AD的中点
求∠AEF的度数
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连接EF.求证:EF=CF.


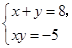

 的解x与y相等,则a的值等于 ( )
的解x与y相等,则a的值等于 ( )
 ,用含x的代数式表示y,得 .
,用含x的代数式表示y,得 . , 则x+y= x-y= .
, 则x+y= x-y= .

 和
和  有公共解,求a,b的值.
有公共解,求a,b的值. 时,如果设
时,如果设 ,则原方程组可变形为关于m、n的方程组
,则原方程组可变形为关于m、n的方程组 。解这个方程组得到它的解为
。解这个方程组得到它的解为 。由
。由 ,求得原方程组的解为
,求得原方程组的解为 。利用上述方法解方程组:
。利用上述方法解方程组:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号