2011-2012学年八年级第二学期期中考试数学卷
“5·12”汶川大地震导致某铁路隧道被严重破坏.为抢修其中一段120米的铁路,施工队每天比原计划多修5米,结果提前4天开通了列车.问原计划每天修多少米?设原计划每天修 米,所列方程正确的是( )
米,所列方程正确的是( )
A. |
B. |
C. |
D. |
下列说法中,正确的是( )
A.满足不等式  的 的 的最大负整数是 的最大负整数是 |
B.若点 、 、 、 、 在双曲线 在双曲线 上,则 上,则 |
C.将双曲线 绕原点旋转90°后,可得到双曲线 绕原点旋转90°后,可得到双曲线 |
D.若双曲线 与直线 与直线 有交点, 则 有交点, 则 |
.已知一次函数 与反比例函数
与反比例函数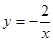 ,
,  与
与 的部分对应值如下表:
的部分对应值如下表:
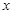 |
-3 |
-2 |
-1 |
-0.5 |
1 |
1.5 |
2 |
3 |
 |
4 |
3 |
2 |
1.5 |
0 |
-0.5 |
-1 |
-2 |
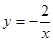 |
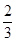 |
1 |
2 |
4 |
-2 |
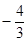 |
-1 |
 |
不解方程,观察上表中的相关数据,可知方程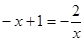 的解为 .
的解为 .
.如图,A、B分别是反比例函数 图象上的点,过A、B作
图象上的点,过A、B作 轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为
轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为 ,四边形ACDE的面积为
,四边形ACDE的面积为 ,则
,则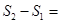 .
.
(本大题10分)已知不等式: ⑴ 1- <0; ⑵
<0; ⑵ 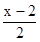 <1; ⑶
<1; ⑶  ;
;
⑷ 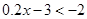 .你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来.
.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来.
(本大题10分)一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;(2)如果该司机匀速返回时,用了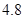 小时,求返回时的速度.
小时,求返回时的速度.
(本大题10分)如果设f(x)= , 那么f(a)表示当x=a时,
, 那么f(a)表示当x=a时, 的值,即f(a)=
的值,即f(a)= ,如:f(1)=
,如:f(1)= =
=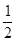 .
.
(1)求f(2) +f (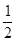 )的值;
)的值;
(2)求f(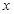 )+f(
)+f(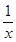 )的值;
)的值;
(3)计算: f(1)+f(2)+f(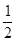 )+f(3)+f(
)+f(3)+f(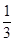 )+…+f(n)+f(
)+…+f(n)+f( ).(结果用含有n的代数式表示,n为正整数)
).(结果用含有n的代数式表示,n为正整数)
(本大题12分)按如图所示的程序进行运算,并回答问题
(1)开始输入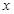 的值为3,那么输出的结果是 ;
的值为3,那么输出的结果是 ;
(2)要使开始输入的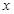 值只经过一次运行就能输出结果,求
值只经过一次运行就能输出结果,求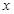 的值取值范围?
的值取值范围?
(3)要使开始输入的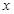 值经过两次运行,才能输出结果,求
值经过两次运行,才能输出结果,求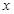 的值取值范围?
的值取值范围?
(本大题12分)反比例函数 与一次函数
与一次函数 的图象交于A(
的图象交于A( ,4)、
,4)、
B(4, )两点.
)两点.
(1)求A、B两点的坐标;
(2)求一次函数解析式;
(3)求△AOB的面积;
(4)当 为何值时,反比例函数的值大于一次函数的值?(直接写出结果)
为何值时,反比例函数的值大于一次函数的值?(直接写出结果)
(本大题12分)某镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:
| 湘 莲 品 种 |
A |
B |
C |
| 每辆汽车运载量(吨) |
12 |
10 |
8 |
| 每吨湘莲获利(万元) |
3 |
4 |
2 |
(1)设装运A种湘莲的车辆数为x,装运B种湘莲的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)在(2)的方案中,若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
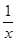 、
、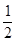
 、
、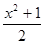 、
、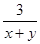 、
、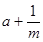 中,分式的个数有( )
中,分式的个数有( ) >
>
 <
<
 的值为0,那么x为( )
的值为0,那么x为( ) 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) 
 和反比例函数
和反比例函数 的一个交点为(1,2),则另一个交点为( )
的一个交点为(1,2),则另一个交点为( ) 与反比例函数
与反比例函数 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )
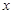 时,分式
时,分式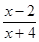 有意义.
有意义.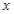 的分式,使此分式当
的分式,使此分式当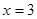 时,它的值为2,这个分式可以是 .
时,它的值为2,这个分式可以是 . 的图象经过点
的图象经过点 ,则
,则 .
. .
. 的分式方程
的分式方程 无解,则
无解,则 的值为 .
的值为 . ,当
,当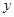 满足 时,有
满足 时,有
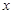 ≤
≤ .
. 与直线
与直线 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于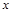 的不等式
的不等式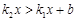 的解集为 .
的解集为 .
 的不等式组
的不等式组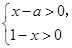 的整数解共有3个,则
的整数解共有3个,则 的取值范围是 .
的取值范围是 .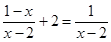 .
. ,求代数式
,求代数式 的值.小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程.
的值.小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号