[广东]2011-2012学年广东省汕头市九年级一元二次方程单元卷.doc
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+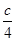 =0的根的情况是( ).
=0的根的情况是( ).
| A.没有实数根 | B.有两个不相等的正实数根 | C.有两个不相等的负实数根 | D.有两个异号实数根 |
下面是某同学在一次数学测验中解答的填空题,其中答对的是( )
| A.若x2=4,则x=2 |
| B.若3x2="6x,则x=2" |
C. 的一个根是1,则k=2 的一个根是1,则k=2 |
D.若分式 的值为零,则x=2 的值为零,则x=2 |
飞机起飞时,首先要在跑道上滑行一段路程,这种运动在物理学上叫匀加速运动,其公式为 。若飞机在起飞前滑行4000米的距离,其中a=20米/秒2 ,则飞机起飞用的时间t= 秒。
。若飞机在起飞前滑行4000米的距离,其中a=20米/秒2 ,则飞机起飞用的时间t= 秒。
在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物—“福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?


 ,下列配方正确的是( )
,下列配方正确的是( ) 
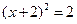


 ,当x>0时,y随x的增大而增大,则关于x的方程
,当x>0时,y随x的增大而增大,则关于x的方程 的根的情况是( )
的根的情况是( ) 的值等于零,则x的值是( )
的值等于零,则x的值是( ) ,若
,若 ,则该方程一定有一个根为( )
,则该方程一定有一个根为( ) 是关于x的一元二次方程,则( )
是关于x的一元二次方程,则( )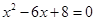 的两个根,则这个三角形的周长是( )
的两个根,则这个三角形的周长是( ) 化为一元二次方程的一般形式是________,它的一次项系数是______.
化为一元二次方程的一般形式是________,它的一次项系数是______. 的值是7,则代数式
的值是7,则代数式 的值是
的值是  的一个根为
的一个根为 ,则
,则
 ,
, 是方程
是方程 的两实数根,则
的两实数根,则 的值为______ .
的值为______ . ,则
,则 __________。
__________。 (配方法) (2)
(配方法) (2)

 .
.
 ;
; 。令
。令 ,原方程化成
,原方程化成


 ;当
;当
 时(不合题意,舍去)
时(不合题意,舍去) 

 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。 粤公网安备 44130202000953号
粤公网安备 44130202000953号