[浙江]2011年浙江省湖州市五校七年级第一学期期中质量调研数学卷
A为数轴上表示-1的点,将A点沿数轴向左移动2个单位长度到B点,则B点所表示的数为( )
| A.3 | B.1 | C.-3 | D.1或-3 |
我国是世界上严重缺水的国家之一,目前我国年可利用的淡水资源总量为27500亿米3,人均占有淡水量居全世界第110位,因此我们要节约用水,27500亿这个数用科学记数法表示并保留两个有效数字为( ).
A. |
B. |
C. |
D. |
估计+1的值是( )
| A.在2和3之间 | B.在3和4之间 | C.在4和5之间 | D.在5和6之间 |
下列说法:①在1和3之间的无理数有且只有 ,
, ,
, ,
, 这4个;②近似数7.30所表示的准确数a的范围是:7.295≤a<7.305;③一个数的绝对值必大于这个数的相反数;④大于-2.5而小于π的整数共有6个;⑤平方根是本身的数是1和0;⑥有理数可以分为正数和负数;⑦
这4个;②近似数7.30所表示的准确数a的范围是:7.295≤a<7.305;③一个数的绝对值必大于这个数的相反数;④大于-2.5而小于π的整数共有6个;⑤平方根是本身的数是1和0;⑥有理数可以分为正数和负数;⑦ 的值是
的值是 或
或 .其中正确的是( )
.其中正确的是( )
| A.5个 | B.4个 | C.3个 | D.2个 |
如图所示,数轴上表示1, ,的点为A,B,且C,B两点到点A的距离相等,则点C所表示的数是 ( )
,的点为A,B,且C,B两点到点A的距离相等,则点C所表示的数是 ( )
A.2- |
B. |
C. |
D. |
如图,点A表示的数是-2,以A点为圆心, 个长度单位长度为半径的圆交数轴于B、C两点,那么B、C两点表示的数分别是___________。
个长度单位长度为半径的圆交数轴于B、C两点,那么B、C两点表示的数分别是___________。
观察下面三行数
1,-2,4,-8,16,-32 ……①
0,-6,6,-18,30,-66 ……②
2,-4,8,-16,32,-64 ……③
取每行数的第8个数,计算它们的和是 。
计算(每小题3分,共 18分,)
(1) (2)
(2)  +(-
+(- )
)
(3) (4)2-
(4)2-
(5)  (6)
(6) 
(本题6分)在如图所示的3×3的方格中,画出3个面积小于9的不同的正方形,同时要求所画正方形的顶点都在方格的顶点上,并且写出边长.
 |
 |
||||
 |
|||||
边长为 边长为 边长为
(本题8分)如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( ,  ),
),
C→ (+1, );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),
(-2,+3),(-1,-2),请在图中标出P的位置。
(本题8分)“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的9 2%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
2%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围(千克) |
0~50 部分 |
50以上~150 部分 |
150以上~250 部分 |
250以上 部分 |
| 价 格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
(1)如果他批发80千克太湖蟹,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克太湖蟹 (150<x<200),请你分别用含字母x的式子表示他在A 、B两家批发所需的费用;
(3)现在他要批发195千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.


 ,
, ,
, ,
, ,
, ,
, 中,无理数的个数是( )
中,无理数的个数是( )




 ,则x-y的值为( )
,则x-y的值为( )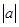 =3,则a的值是 .
=3,则a的值是 . ______0;(2)0.05______-∣-1∣;(3)
______0;(2)0.05______-∣-1∣;(3) _
_ _____
_____
 ,则x= , 若
,则x= , 若 ,则x= .
,则x= . 为实数,且
为实数,且 ,则(x+y)2011的值为________.
,则(x+y)2011的值为________. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号