山东省日照市莒县第三协作区八年级上期中数学试卷
下列计算中正确的是( ).
| A.a2+b3=2a5 | B.a4÷a=a4 |
| C.a2·a4=a8 | D.(-a2)3=-a6 |
下列各式中能用平方差公式的是( )
| A.(x+y)(y+x) | B.(x+y)(y-x) |
| C.(x+y)(-y-x) | D.(-x+y)(y-x) |
如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( ).
| A.0 | B.3 | C.-3 | D.1 |
等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为 ( )
| A.30° | B.60° | C.60°或120° | D.30°或150° |
若(x-3)(x+4)=x2+px+q,那么p、q的值是( )
| A.p=1,q=-12 | B.p=-1,q=12 |
| C.p=7,q=12 | D.p=7,q=-12 |
如图,△ 中
中 平分
平分 ,过
,过 作直线平行于
作直线平行于 ,交
,交 于
于 ,当
,当 的位置及大小变化是,线段
的位置及大小变化是,线段 和
和 的大小关系是 ( )
的大小关系是 ( )

A. |
B. |
C. |
D.不能确定 |
已知点A(x,-4)与点B(3,y)关于x轴对称,那么x+y的值为____________.
有一个分式,三位同学分别说出了它的一些特点,甲:分式的值不可能为0;乙:分式有意义时的取值范围是≠±1;丙:当=-2时,分式的值为1.请你写出满足上述全部特点的一个分式: .
分解因式:
(1)2a3-12a2+18a
(2)9a2(x-y)+4b2(y-x)
先化简,再求值.
已知x2﹣5x﹣14=0,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE.求∠CDE的度数.
如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
| A.提取公因式 |
| B.平方差公式 |
| C.两数和的完全平方公式 |
| D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.

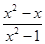 的值为零的所有
的值为零的所有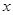 的值是( )
的值是( )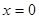

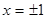
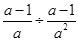 的结果是( ).
的结果是( ).
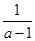
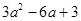 = .
= . 中,
中, ,
, 平分
平分 ,若
,若 ,则
,则 = .
= .
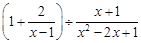 的结果是 .
的结果是 . ,则
,则 =_____________.
=_____________.

 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号