北师大版选修1-2 1.1回归分析练习卷
根据如下样本数据:
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
﹣0.5 |
0.5 |
﹣2.0 |
﹣3.0 |
得到回归方程为 =bx+a,则( )
=bx+a,则( )
A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0
已知变量x与y正相关,且由观测数据算得样本平均数 =3,
=3, =3.5,则由该观测数据算得的线性回归方程可能是( )
=3.5,则由该观测数据算得的线性回归方程可能是( )
A. =0.4x+2.3 =0.4x+2.3 |
B. =2x﹣2.4 =2x﹣2.4 |
C. =﹣2x+9.5 =﹣2x+9.5 |
D. =﹣0.3x+4.4 =﹣0.3x+4.4 |
根据如下样本数据,得到回归方程 =bx+a,则( )
=bx+a,则( )
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
﹣0.5 |
0.5 |
﹣2.0 |
﹣3.0 |
A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0
在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都恰好在直线 上,则这组样本数据的样本相关系数为( )
上,则这组样本数据的样本相关系数为( )
| A.﹣1 | B.0 | C. |
D.1 |
下列说法中错误的是( )
A.线性回归方程中,对于x的预报值 与实际值y未必相等 与实际值y未必相等 |
B.在频率分布直方图中,中位数左边的直方图的面积为 |
| C.在设计抽样方法时,应该使每个个体有同样的机会被抽中 |
| D.甲、乙两个模型的R2分别约为0.98和0.80,则模型乙的拟合效果更好 |
观察下列关于变量x和y的三个散点图,它们从左到右的对应关系依次是( )
| A.正相关、负相关、不相关 |
| B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 |
| D.正相关、不相关、负相关 |
如图是根据变量x,y的观测数据(xi,yi)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
| A.①② | B.①④ | C.②③ | D.③④ |
为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线 =bx+a近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )
=bx+a近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )
| A.线性相关关系较强,b的值为1.25 |
| B.线性相关关系较强,b的值为0.83 |
| C.线性相关关系较强,b的值为﹣0.87 |
| D.线性相关关系太弱,无研究价值 |
对具有线性相关关系的变量x,y,有一组观测数据(xi,yi)(i=1,2,…,8),其回归直线方程是: =
= x+a,且x1+x2+x3+…+x8=3(y1+y2+y3+…+y8)=6,则实数a的值是( )
x+a,且x1+x2+x3+…+x8=3(y1+y2+y3+…+y8)=6,则实数a的值是( )
A. |
B. |
C. |
D. |
已知x、y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且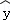 =0.95x+a,则a=( )
=0.95x+a,则a=( )
A.1.30 B.1.45 C.1.65 D.1.80
在一次实验中,测得(x,y)的四组值为(1,2),(2,3),(3,4),(4,5),则y与x之间的回归直线方程为( )
A. =x+1 =x+1 |
B. =x+2 =x+2 |
C. =2x+1 =2x+1 |
D. =x﹣1 =x﹣1 |
某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
| x |
16 |
17 |
18 |
19 |
| y |
50 |
34 |
41 |
31 |
由上表,可得回归直线方程 中的
中的 =﹣4,据此模型预计零售价定为15元时,每天的销售量为( )
=﹣4,据此模型预计零售价定为15元时,每天的销售量为( )
A.48个 B.49个 C.50个 D.51个
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系,对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 =kx+a,则点(a,b)与直线x+18y=100的位置关系是( )
=kx+a,则点(a,b)与直线x+18y=100的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
已知具有线性相关的两个变量x,y之间的一组数据如下:
| x |
0 |
1 |
2 |
3 |
4 |
| y |
2.2 |
4.3 |
4.5 |
4.8 |
6.7 |
且回归方程是 =0.95x+a,则当x=6时,y的预测值为( )
=0.95x+a,则当x=6时,y的预测值为( )
A.8.0 B.8.1 C.8.2 D.8.3
在2013年9月15日,某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归方程是:y=﹣3.2x+a,则a=( )
A.﹣24 B.35.6 C.40.5 D.40
某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
| 月平均气温x(℃) |
17 |
13 |
8 |
2 |
| 月销售量y(件) |
24 |
33 |
40 |
55 |
由表中数据算出线性回归方程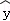 =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46 B.40 C.38 D.58





 ,则b=( )
,则b=( ) B.
B. C.
C. D.
D.
 =1.23x+4
=1.23x+4 粤公网安备 44130202000953号
粤公网安备 44130202000953号