江苏省江阴市要塞片八年级上学期期中考试数学试卷
有下列长度的三条线段,能组成等腰三角形的是( )
| A.2cm,2cm,4cm |
| B.3cm,8cm,3cm |
| C.3cm,4cm,6cm |
| D.5cm,4cm,4cm |
如图,下列条件中,不能证明△ABD≌△ACD的是( )
| A.AB=AC ,BD=CD |
| B.∠B=∠C,∠BAD=∠CAD |
| C.∠B=∠C,BD=CD |
| D.∠ADB=∠ADC,DB=DC |
给出的下列说法中:①以1 ,2, 为三边长的的三角形是直角三角形;②如果直角三角形的两边长分别是3和4,那么斜边必定是5;③一个等腰直角三角形的三边长分别是a、b、c,其中c为斜边,那么a︰b︰c=1︰1︰
为三边长的的三角形是直角三角形;②如果直角三角形的两边长分别是3和4,那么斜边必定是5;③一个等腰直角三角形的三边长分别是a、b、c,其中c为斜边,那么a︰b︰c=1︰1︰ .其中正确的是( )
.其中正确的是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
等腰三角形有一个角为50°,则它的顶角度数是( )
| A.50° | B.65° | C.80° | D.50°或80° |
小明不慎将一块三角形的玻璃摔碎成四块(即图中标有1、2、3、4的四块),如果将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带 ( ) 
| A.第1块 | B.第2块 | C.第3块 | D.第4块 |
如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
| A.7cm | B.10cm | C.12cm | D.22cm |
如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
| A.△ABC三条中线的交点 |
| B.△ABC三边的垂直平分线的交点 |
| C.△ABC三条高所在直线的交点 |
| D.△ABC三条角平分线的交点 |
如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是 ( )
A. |
B. |
C.1 | D. |
如图,∠AOB=45°,在OA上截取OA1=1,OA2=3,OA3=5,OA4=7,OA5=9,,过点A1、A2、A3、A4、A5分别作OA的垂线与OB相交,得到并标出一组阴影部分,它们的面积分别为S1,S2,S3,.观察图中的规律,第n个阴影部分的面积Sn为 ( )
| A.8n-4 | B.4n | C.8n+4 | D.3n+2 |
如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 . (只添一个条件即可).
在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为__________.
如图,以直角三角形一边向外作正方形,其中两个正方形的面积为100和64,则正方形A的面积为 .
如图,把一张直角三角形纸片按照图①~③的过程折叠.若直角三角形的两条直角边分别是5和12,则最后折成的图形的面积(按单层计算)为 .
如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC.若AC=4,BC=3,AB=5,则OC的长度的最大值是 .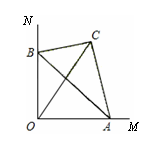
(1)画出△ABC关于直线MN的对称图形△A´B´C´.

(2)如图:某通信公司在A区要修建一座信号发射塔M,要求发射塔到两城镇P、Q的距离相等,同时到两条高速公路l1、l2的距离也相等.在图中作出发射塔M的位置.(不写作法,保留作图痕迹)

请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
已知:如图,同一直线上有四点B、E、C、F,且 AB∥DE,AC∥DF,BE=CF.
请说明:AB=DE.
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.
如图,直角三角形的两直角边AC="6" cm,BC="8" cm,沿AD折叠使AC落在AB上.点C与E重合,折痕为AD,试求CD的长.
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC= .现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
在△ABC中, AB、BC、AC三边的长分别为 、
、 、
、 ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为: .
(2)若△DEF三边的长分别为 、
、 、
、 ,请在图2的正方形网格中画出相应的
,请在图2的正方形网格中画出相应的
△DEF,并利用构图法求出它的面积为_____________.
(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是 m2.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号