如图,椭圆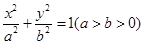 的一个焦点是
的一个焦点是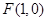 ,
, 为坐标原点.
为坐标原点.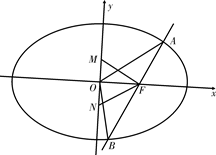
(1)已知椭圆短轴的两个三等分点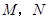 与一个焦点构成正三角形,求椭圆的方程;
与一个焦点构成正三角形,求椭圆的方程;
(2)设过点 的直线
的直线 交椭圆于
交椭圆于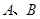 两点.若直线
两点.若直线 绕点
绕点 任意转动,则有
任意转动,则有 ,求
,求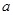 的取值范围.
的取值范围.
已知圆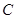 :
: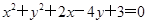 .
.
(1)若圆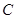 的切线在
的切线在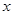 轴和
轴和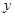 轴上的截距相等,求此切线的方程.
轴上的截距相等,求此切线的方程.
(2)从圆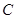 外一点
外一点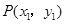 向该圆引一条切线,切点为
向该圆引一条切线,切点为 为坐标原点,且有
为坐标原点,且有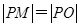 ,求使得
,求使得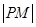 取得最小值的点
取得最小值的点 的坐标.
的坐标.
已知直线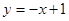 与椭圆
与椭圆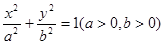 相交于
相交于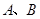 两点.
两点.
(Ⅰ)若椭圆的离心率为 ,焦距为2,求线段
,焦距为2,求线段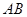 的长;
的长;
(Ⅱ)若向量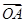 与向量
与向量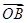 互相垂直(其中
互相垂直(其中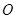 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率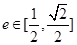 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.
已知圆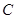 的圆心为
的圆心为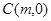 ,
,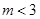 ,半径为
,半径为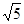 ,圆
,圆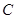 与离心率
与离心率 的椭圆
的椭圆 的其中一个公共点为
的其中一个公共点为 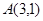 ,
,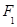 、
、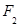 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆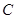 的标准方程;
的标准方程;
(2)若点 的坐标为
的坐标为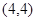 ,试探究直线
,试探究直线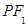 与圆
与圆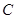 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆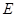 和直线
和直线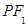 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
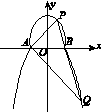
如图所示,曲线C由部分椭圆C1: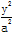 +
+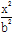 =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为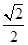 .
.
(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l
的方程.
若a>0,b>0,且函数f(x)=4x3-ax2-bx+2在x=1处有极值,则ab的最大值等于( )
| A.4 | B.8 | C.9 | D.18 |
如图所示,平面
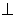 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形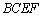 为直角梯形,
为直角梯形,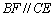 ,
,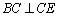 ,
,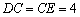 ,
, .
.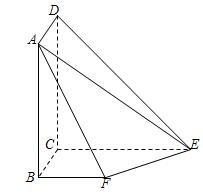
(1)求证: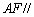 平面
平面 ;
;
(2)求平面 与平面
与平面 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(3)求直线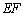 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知椭圆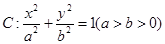 的左、右焦点分别是
的左、右焦点分别是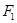 ,
,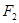 ,如果椭圆
,如果椭圆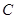 上的动点到点
上的动点到点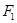 的距离的最大值是
的距离的最大值是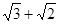 ,短轴一个端点到点
,短轴一个端点到点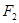 的距离为
的距离为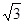 .
.
(1)求椭圆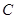 的方程;
的方程;
(2)设过点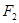 且斜率为
且斜率为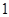 的直线
的直线 与椭圆
与椭圆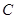 交于
交于 、
、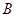 两点,求
两点,求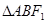 的面积.
的面积.
根据表格内的数据,可以断定方程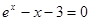 的一个根所在区间是( )
的一个根所在区间是( )
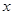 |
-1 |
0 |
1 |
2 |
3 |
 |
0.37 |
1 |
2.72 |
7.39 |
20.08 |
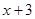 |
2 |
3 |
4 |
5 |
6 |
A、
B、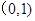
C、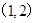
D、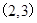
为了了解某工业园中员工的颈椎疾病与工作性质是否有关,在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查,得到如下的列联表.
| |
患有颈椎疾病 |
没有患颈椎疾病 |
合计 |
| 白领 |
|
5 |
|
| 蓝领 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人,抽到患有颈椎疾病的人的概率为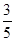 .
.
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为患颈椎疾病与工作性质有关?说明你的理由;
(2)已知在患有颈椎疾病的10名蓝领中,有3为工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为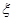 ,求
,求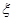 的分布列及数学期望.
的分布列及数学期望.
参考公式: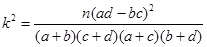 ,其中
,其中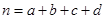 .
.
下面的临界值表仅供参考:
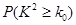 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
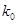 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |