一个底面积为2×10-2 m2的薄壁圆柱形容器放在水平桌面中央,容器高为0.12 m,内盛有0.08 m深的水,如下图(a)所示,另有质量为0.8kg,体积为1×10-3 m3的实心正方体A,如图(b)所示(取g=10N/kg)。求: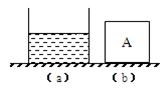
(1)实心正方体A的密度;
(2)将实心正方体A放入图(a)的水中后,正方体A所受浮力
(3)将实心正方体A放入图(a)的水中后,水对容器底部的压强变化了多少?
在水平桌面上放有一柱形容器,底面积为500cm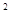 ,里面装有深度为20cm的水;一个重力为2N的开口玻璃杯A,其底部与一个体积为50cm
,里面装有深度为20cm的水;一个重力为2N的开口玻璃杯A,其底部与一个体积为50cm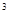 重力为3.9N的实心铁块B用细线相连(细线的质量体积忽略不计),然后放入水中,但在放入过程中由于不小心,容器中有少量的水流入了玻璃杯中,最后A、B两物体在水中处于静止,如图所示,此时玻璃杯A排开水的体积为640cm
重力为3.9N的实心铁块B用细线相连(细线的质量体积忽略不计),然后放入水中,但在放入过程中由于不小心,容器中有少量的水流入了玻璃杯中,最后A、B两物体在水中处于静止,如图所示,此时玻璃杯A排开水的体积为640cm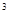 。求:
。求:
(1)没有放入玻璃杯和铁块时水对容器底部的压强;
(2)A、B两物体在水中静止时细线对铁块B的拉力;
(3)若细线突然断开,A、B两物体再一次静止后(这个过程中玻璃杯A开口始终向上),水对容器底部的压强为多少?
如图所示,底面积为2×10(2米2的圆柱形平底薄壁水槽放在水平地面上,一装有金属球的小盆漂浮在水槽的水面上,小盆的质量为1千克,金属球的质量为1.6千克,金属球的体积为0.2×10(3米3。
① 若把金属球从盆中拿出并放入水槽中后,小球沉入水底,求容器对水平地面压强的变化量。
② 求水对水槽底部的压强变化量。
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有 的体积浸在水中,此时弹簧恰好处于自然状态,即没有发生形变(已知水的密度为1.0×103kg/m3,不计弹簧所受的浮力,g取10N/kg)
的体积浸在水中,此时弹簧恰好处于自然状态,即没有发生形变(已知水的密度为1.0×103kg/m3,不计弹簧所受的浮力,g取10N/kg)
⑴求此时容器底部受到水的压强;
⑵求木块A的密度;
⑶先向容器内缓慢加水,直至木块A刚好完全浸没在水中,此时弹簧对木块的作用力为F1,再打开阀门B缓慢放水,直至木块A完全离开水面时,再关闭阀门B,此时弹簧对木块A的作用力为F2,求F1与F2之比。
底面积为 的圆柱形容器内装有适量的水,将其竖直放在水平桌面上,把边长为
的圆柱形容器内装有适量的水,将其竖直放在水平桌面上,把边长为 的正方体木块A放入水后,再在木块A的上方放一物体B,物体B恰好没入水中,如图所示.已知物体B的密度为
的正方体木块A放入水后,再在木块A的上方放一物体B,物体B恰好没入水中,如图所示.已知物体B的密度为 .质量为
.质量为 .
.
求:(1)物体B的体积;
(2)木块A的密度;
(3)若将B放入水中,如图(b)所示,请分析出液面的变化情况;
(4)并求此时水对容器底部压强的变化值.
如图所示,底面积为200cm2的容器底部有一固定轻质弹簧,弹簧上方连有一边长为10cm的正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg)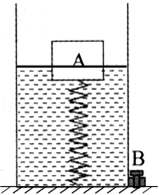
求:(1)此时容器底部受到的水的压强;
(2)木块A的密度;
(3)向容器内缓慢加水,直至木块A刚好完全浸没水中,立即停止加水,弹簧伸长了3cm,求此时弹簧对木块A的作用力F1是多大?容器底部受到水的压强变化了多少?
科学家在进行海洋科考时,常用到一个很大的浮筒.浮筒是由一个质量为90kg的空心圆柱形铁罐制成的,铁罐高2.1m,底面积0.08m2.把浮筒至于海面时,它的一端浮出水面,上方可安装无线电转播器.某次科考中,工作人员装好无线电转播器,将浮筒竖直漂浮在海面上,浮筒露出水面的高度(不含无线电转播器的高度)为0.6m.如图所示.(海水取1.0×103kg/m3,g取10N/kg)求:
(1)浮筒底部所受海水的压强.
(2)浮筒受到的浮力.
(3)安装的无线电转播器的质量.
如图所示,容器中装有水,水中有一个木块被细线系着,已知水重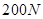 ,水深为
,水深为 ,木块的体积为
,木块的体积为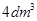 ,木块的密度为
,木块的密度为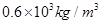 ,试求:
,试求: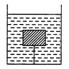
(1)水对容器底面的压强是多少?木块受到的浮力是多大?
(2)若绳子断了,最终木块漂浮在水面上时,所受的浮力为多大?此时水对容器底的压强比第(1)问中的大还是小?(g取10N/kg)
平底茶壶的质量是400g,底面积是40cm2,内盛0.6kg的开水,放置在面积为1m2的水平桌面中央。(g取10N/kg)试求:
(1)茶壶对桌面的压强。
(2)水对茶壶底部的压力;
在水平桌面上放置一空玻璃杯,它的底面积为0.01 m2,它对桌面的压强为200Pa.(g取10 N/kg,杯壁的厚度可忽略)
(1)求玻璃杯的质量.
(2)在玻璃杯中装入1 kg水后,水对杯底的压强为900 Pa,求水的深度.
(3)玻璃杯的大致形状是图中a、b、c中的哪一种?
如图(a)所示,轻质薄壁圆柱形容器甲置于水平地面,底面积为 ,容器高0.2米,内盛0.15米深的水。
,容器高0.2米,内盛0.15米深的水。
① 若容器的底面积为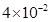 米2,求容器中水的质量
米2,求容器中水的质量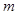 。
。
② 求0.1米深处水的压强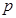 。
。
③ 现有面积为 、密度为
、密度为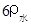 圆柱体乙,如图(b)所示,在乙上方沿水平方向切去高为
圆柱体乙,如图(b)所示,在乙上方沿水平方向切去高为 的部分A(
的部分A(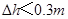 ),如图(c)所示,将A放入容器甲中(A与甲底部没有密合),并将此时的容器置于剩余圆柱体B的上方中央。
),如图(c)所示,将A放入容器甲中(A与甲底部没有密合),并将此时的容器置于剩余圆柱体B的上方中央。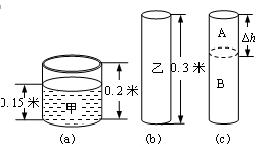
(a)若要使水对容器底部的压强 最大,求切去部分A高度的最小值
最大,求切去部分A高度的最小值 。
。
(b)若要使水对容器底部的压强 与地面受到的压强
与地面受到的压强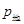 的比值最大,求切去部分A高度
的比值最大,求切去部分A高度 的范围,并求比值
的范围,并求比值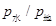 。
。
如图所示,轻质柱形容器甲、乙放置在水平地面上,已知甲、乙的底面积分别为2S、S。甲容器中装有3×10-2米3的水,A点离水面0.2米。
(1)求甲容器中的水的质量,A点水的压强。
(2)将乙容器中注入密度为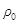 的液体后,甲、乙两液面相平,深度均为
的液体后,甲、乙两液面相平,深度均为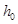 ,再将密度为
,再将密度为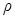 、体积为
、体积为 的物体A放入甲容器中,将密度为
的物体A放入甲容器中,将密度为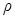 、体积为
、体积为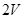 的物体B放入乙容器中(液体不溢出)。已知甲容器对地面的压强是乙容器对地面压强的3倍。求
的物体B放入乙容器中(液体不溢出)。已知甲容器对地面的压强是乙容器对地面压强的3倍。求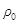 的表达式
的表达式
质量为1千克的柱形薄壁容器放在水平面上,底面积为0.01米2,高为0.6米,装有0.5米深的酒精(ρ酒精=0.8×103千克/米3), 如图所示。求:

①酒精对容器底部的压强。
②容器对水平面的压强。
③在酒精中放入一个固体,保持酒精不溢出,使酒精对容器底部压强的增加量最大的情况下,同时使容器对水平面压强的增加量最小,请计算固体的质量并判断固体密度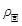 与酒精密度
与酒精密度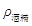 之间的大小关系,即
之间的大小关系,即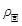
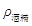 。
。
如图所示,质量均为2.4千克的薄壁圆柱形容器A和B放在水平地面上,底面积分别为2×10-2米2和1×10-2米2。容器A中盛有0.1米高的水,容器B中盛有质量为1.6千克的酒精。(ρ酒精=0.8×103千克/米3)求: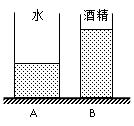
①容器B中酒精的体积V酒精。
②容器B对水平地面的压强pB。
③现有质量相等的甲、乙两实心物块,若将甲浸没在水中、乙浸没在酒精中后,两液体均未溢出,且两液体各自对容器底部压强的变化量相等,求甲、乙的密度ρ甲、ρ乙之比。
我国从20世纪70年代开始大规模研制潜水器,现已达到国际领先水平。2010年7月下水的“蛟龙号”深海潜水器,是我国自主研制的,其设计下潜深度达7 000 m。2011年7月已完成5000 m级深海潜海和科学探测.若“蛟龙号”潜水器下潜至5 000 m,求:
(1)它受到的海水压强大约是多少?(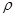 海水=1.03×103 kg/m3,g取10N/kg)
海水=1.03×103 kg/m3,g取10N/kg)
(2)若观察窗面积为300 cm2,海水对观察窗的压力大约是多少?