初中数学填空题

如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，3）,C（n，-5），A（4，0），则AD·BC=          ．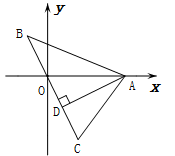

我们把所有正奇数按照从小到大的顺序排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…现用等式An=（a，b）表示奇数x是第a组第b个数（从左往右数），如A₇=（2，3），A₂₃=（4，4），则A₂₀₁₅=          ．

．如图，在△ABC中，∠C=90°，AC=BC=2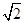，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；
②四边形CEDF的周长不变；
③点C到线段EF的最大距离为1．
其中正确的结论有             ．（填写所有正确结论的序号）

将两个斜边长相等的直角三角形纸片如图①放置，其中∠ACB=∠CED=90°．∠A=45°，∠D=30°．

（1）∠CBA=           ；
（2）把△DCE绕点C顺时针旋转15°得到△D₁CE₁，如图②，连接D₁B，则∠E₁D₁B=               ．

在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S_△ADE：S_{四边形BCED}=1：8，则AD=     cm．

如图，点A在双曲线y=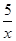上，点B在双曲线y=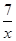上，且AB∥x轴，C、D在x轴上，若四边形ABCD为平行四边形，则它的面积为             ．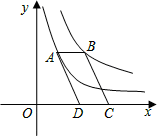

如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是         ．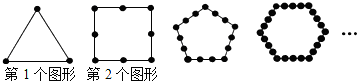

有一个十进制的六位数（其中a、b、c、d、e分别是这个六位数的万位、千位、百位、十位、个位上的数字）乘以3后，变成一个新的六位数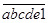，则原来的六位数是            ．

如图，直线与坐标轴交于AB两点，点是轴上一动点，以点M为圆心，2个单位长度为半径作⊙M，当⊙M与直线想切时，的值为__________________．

如图，矩形OABC的顶点A，C的坐标分别是（4，0）（0，2），反比例函数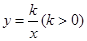的图像过对角线的交点P并且与AB，BC分别交于D，E两点，连接OD，OE，DE，则⊿ODE的面积为_____________．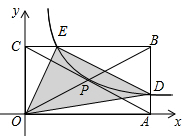

如图，△ABC是边长为1的等边三角形，BD为AC边上的高，将△ABC折叠，使点B与点D重合，折痕EF交BD于点D₁，再将△BEF折叠，使点B于点D₁重合，折痕GH交BD₁于点D₂，依次折叠，则BD_n=    ．

某校数学兴趣小组要测量西山植物园蒲宁之珠的高度．如图，他们在点A处测得蒲宁之珠最高点C的仰角为45°，再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°，AB=62m，根据这个兴趣小组测得的数据，则蒲宁之珠的高度CD约为         m．（sin56°≈0.83，tan56°≈1.49，结果保留整数）

观察下列图形规律：当n=    时，图形“●”的个数和“△”的个数相等．

请看杨辉三角（1），并观察下列等式（2）：

根据前面各式的规律，则（a+b）⁶=                       ．

如图是由等圆组成的一组图，第①个图由1个圆组成，第②个图由5个圆组成，第③个图由12个圆组成…按此规律排列下去，则第⑥个图由       个圆组成．