初中数学填空题

如图，△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，若CD＝3，则点D到AB的距离是      ．

如图6，直角坐标系中一条圆弧经过网格点A，B，C，其中B点坐标为（4，4），则该圆弧所在圆的圆心坐标为              ．

有一张一个角为30°，最小边长为4的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是             ．

如图，矩形ABCD的对角线AC=10，BC=8，则图中五个小矩形的周长之和为_______．

=                     ．

观察下列等式：
第1个等式：x₁=；
第2个等式：x₂=；
第3个等式：x₃=；
第4个等式：x₄=；
则x_l+x₂+x₃+…+x₁₀=                ．

（本题8分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：

（1）从中取出2张卡片，使这2张卡片上数字的乘积最小，乘积的最小值为            ；
（2）从中取出4张卡片，用学过的运算方法，使结果为24。写出运算式子。
（写出一种即可）算24的式子为                                             。

已知，四边形ABCD，连接AC，∠ABC=∠BAC=∠DAC=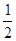∠ADC，若DC=2AD=4，则△ABC的面积为_____________．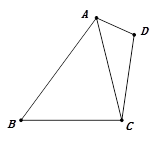

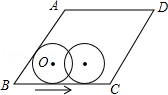
如图，菱形ABCD的边长为8cm，∠BAD=120°，半径为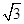cm的⊙O在其内部逆时针连续滚动，且总是保持与菱形ABCD的边相切，当⊙O第一次回到起始位置时，圆心O所走过的路程长度为      cm．

已知，如图直线l的解析式为y=x+4，交x、y轴分别于A、B两点，点M（-1，3）在直线l上，O为原点．

（1）点N在x轴的负半轴上，且∠MNO=60°，则AN=       ；
（2）点P在y轴上，线段PM绕点P旋转60°得到线段PQ，且点Q恰好在直线l上，则点P的坐标为      或        ．

王翔同学在一次跳高训练中采用了背跃式，跳跃路线正好和抛物线y=-2+3x+相吻合，那么他能跳过的最大高度为_________m．

如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH，如此下去…．若正方形ABCD的边长记为a₁，按上述方法所作的正方形的边长依次为a₂，a₃，a₄，…，a_n，则a_n=          ．

在平面直角坐标系中，A（2，0）、B（0，3），过点B作直线∥x轴，点P（a，3）是直线上的动点，以AP为边在AP右侧作等腰RtAPQ，∠APQ=Rt∠，直线AQ交y轴于点C．

（1）当a=1时，则点Q的坐标为     ；
（2）当点P在直线上运动时，点Q也随之运动．当a=    时，AQ+BQ的值最小为     ．

如图，平行四边形ABCD中，AB=5，AD=7，AB⊥AC，点E在边AD上，满足=，点F在AB上，满足 =，连结BE和CF相交于点G，则线段CG的长度是     ．

如图，点A在双曲线y=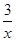第三象限的分支上，连结AO并延长交第一象限的图象于点B，画BC∥x轴交反比例函数y=的图象于点C，若△ABC的面积为6，则k的值是    ．