如图,将边长为 的正方形 折叠,使得 点落在 上的 点,然后压平得折痕 ,若 ,求线段 之长.

以四边形 的边 为斜边分别向外侧作等腰直角三角形,直角顶点分别为 ,顺次连接这四个点,得四边形 .
(1)如图①,当四边形 为正方形时,我们发现四边形 是正方形;
如图②,当四边形 为矩形时,请判断:四边形 的形状(不要求证明);
(2)如图③,当四边形 为一般平行四边形时,设 .
①试用含 的代数式表示 ;
②求证: ;
③四边形 是什么四边形?并说明理由.

如图,设 为等腰直角三角形 斜边 上任意一点, 于点 于点 于 点, 交 于点 ,延长 并在其延长线上取一点 ,使得 .求证: ,且 .

在 中, ,点 分别是 , 的中点, 是等腰三角形, ,连接 .
(1)判断线段 和 的关系,并证明你的结论;
(2)连接 ,过点 作 ,过点 作 和 相交于点 ,在图中先补充图形,再判断四边形 的形状,并证明你的结论.

已知,如图,在菱形 中, 为边 的中点, 与对角线 交于点 ,过 作 于点 .

(1)若 ,求 的长;
(2)求证: .
现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.

下面有四个命题:
(1)一组对边相等且一组对角相等的四边形是平行四边形.
(2)一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
(3)一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形是平行四边形.
(4)一组对角相等且这一组对角的顶点所连接的对角线被另一条对角线平分的四边形是平行四边形.
上述命题是否正确?正确的请证明,错误的请举出反例.
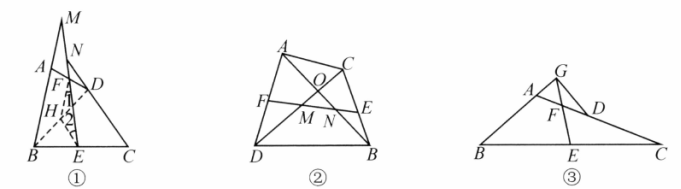
如图①,在四边形 中, 分别是 的中点,连接 并延长,分别与 的延长线交于点 ,则 .
(温馨提示:在图①中,连接 ,取 的中点 ,连接 ,根据三角形中位线定理,证明 ,从而 ,再利用平行线性质,可证 .)
(1)如图②,在四边形 中, 与 相交于点 分别是 的中点,连接 ,分别交 于点 ,判断 的形状,并给予证明;
(2)如图③,在 中, 点在 上, 分别是 的中点,连接 并延长,与 的延长线交于 ,若 ,连接 ,判断 的形状并证明.
设直角三角形的两条直角边长分别为 斜边长为 若 均为正数,且 ,求满足条件的直角三角形的个数.
几何模型:
条件:如图①, . 是直线 同旁的两个定点
问题:在直线 上确定一点 ,使 的值最小.
方法:作点 关于直线 的对称点 ,连接 交 于点 ,则 的值最小(不必证明).
模型应用:
(1)如图②,正方形 的边长为 , 为 的中点, 是 上一动点.连接 ,由正方形对称性可知, 与 关于直线 对称.连接 交于 于 ,则 的最小值是_____;
(2)如图③, 是 内一点, 分别是 上的动点,求 周长的最小值.
