初中数学解答题

某商场计划采购甲、乙、丙三种型号的“格力”牌空调共 $25$台.三种型号的空调进价和售价如下表：

商场计划投入总资金 $5$万元，所购进的甲、丙型号空调数量相同，乙型号数量不超过甲型号数量的一半，若设购买甲型号空调 $x$台，所有型号空调全部售出后获得的总利润为 $W$元.

（1）求 $W$ 与 $x$之间的函数关系式；

（2）商场如何采购空调才能获得最大利润

（3）由于原材料上涨，商场决定将丙型号空调的售价提高 $a$元（ $a\ge 100$），其余型号售价不变，则商场又该如何采购才能获得最大利润？

如图，从如图①所示的等边三角形开始，把它各边分成相等的三段，在中间一段上向外画出一个小等边三角形，形成如图②所示的六角星图形；再在六角星各边上用同样的方法向外画出更小的等边三角形，形成如图③所示的有 $18$个尖角的图形，然后，在其各边上再用同样的方法向外画出更小的等边三角形如图④，如此继续下去，图形的轮廓就能形成分支越来越多的曲线，这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线.

如果设原等边三角形的边长为 $a$，不妨把每一次图形的变化过程叫做“生长”，例如第一次生长后得到图②，每个小等边三角形的边长为 $\frac{1}{3}a$，所形成的图形的周长为 $4a$，请填写下表（用含 $a$的代数式表示）.

	第一次生长后	第二次生长后	第三次生长后	…	第 $n$次生长后
每个小等边三角形的边长	$\frac{1}{3}a$			…
所形成图形的周长	$4a$			…

有 $200$名待业人员参加某企业甲、乙、丙三个部门招聘，到各部门报名的人数百分比见图表①，该企业各部门的录取率见图表②（ $\mathit{部门录取率}=\frac{\mathit{部门录取人数}}{\mathit{部门报名人数}}\times 100\%$）

（1）到乙部门报名的人数有＿＿＿＿＿人，乙部门的录取人数是＿＿＿＿＿人，该企业的录取率为＿＿＿＿＿；

（2）如果到甲部门报名的人员中有一些人员改到丙部门报名，在保持各部门录取率不变的情况下，该企业的录取率将恰好增加 $15\%$，问有多少人从甲部门改到丙部门报名？

（1）如图①， $△\mathit{ABC}$的面积是 $10$，点 $E$是 $\mathit{BC}$的中点，连接 $\mathit{AE}\mathrm{，}△\mathit{AEC}$的面积是＿＿＿＿＿.

（2）如图②，四边形 $\mathit{ABCD}$的面积是 $10$，点 $E\mathrm{，}F$分别是一组对边 $\mathit{AB}\mathrm{，}\mathit{CD}$的中点，连接 $\mathit{AF}\mathrm{，}\mathit{CE}$，则四边形 $\mathit{AECF}$的面积是＿＿＿＿＿.

（3）如图③，点 $E\mathrm{，}F$分别是一组对边 $\mathit{AB}\mathrm{，}\mathit{CD}$上的点，且 $\mathit{AE}=\frac{1}{3}\mathit{AB}\mathrm{，}\mathit{CF}=\frac{1}{3}\mathit{CD}$，若四边形 $\mathit{ABCD}$的面积是 $10$，连接 $\mathit{AF}\mathrm{，}\mathit{CE}$，则四边形 $\mathit{AECF}$的面积是＿＿＿＿＿.

（4）如图④， $\mathrm{◻}\mathit{ABCD}$的面积是 $2\mathrm{，}\mathit{AB}=a\mathrm{，}\mathit{BC}=b$，点 $E$从点 $A$出发沿 $\mathit{AB}$以每秒 $v$个单位长的速度向点 $B$运动，点 $F$从点 $B$出发沿 $\mathit{BC}$以每秒 $\frac{\mathit{bv}}{a}$个单位长的速度向点 $C$运动.点 $E\mathrm{，}F$分别从点 $A\mathrm{，}B$同时出发，当其中一点到达端点时，另一点也随之停止运动.请问四边形 $\mathit{DEBF}$的面积的值是否随着时间 $t$的变化而变化?若不变，请求出这个值；若变化，说明怎样变化的.

问题探究：

（1）请你在图①中做一条直线，使它将矩形 $\mathrm{ABCD}$分成面积相等的两部分；

（2）如图②，点 $\mathrm{M}$是矩形 $\mathrm{ABCD}$内一点，请你在图②中过 $\mathrm{M}$点作一条直线，使它将矩形 $\mathrm{ABCD}$分成面积相等的两部分.

问题解决：

（3）如图③，在平面直角坐标系 $\mathrm{xOy}$中，多边形 $\mathrm{OAB}-\mathrm{CDE}$的顶点坐标分别是 $\mathrm{O}\mathrm{（}0\mathrm{，}0\mathrm{），}\mathrm{A}\mathrm{（}0\mathrm{，}6\mathrm{），}\mathrm{B}\mathrm{（}4\mathrm{，}6\mathrm{），}\mathrm{C}\mathrm{（}4\mathrm{，}4\mathrm{），}\mathrm{D}\mathrm{（}6\mathrm{，}4\mathrm{），}\mathrm{E}\mathrm{（}6\mathrm{，}0\mathrm{）}$.若直线 $\mathrm{l}$经过点 $\mathrm{M}\mathrm{（}2\mathrm{，}3\mathrm{）}$，且将多边形 $\mathrm{OABCDE}$分割成面积相等的两部分，求直线 $l$的函数表达式.

如图，四边形 $\mathrm{EFGH}$是正方形 $\mathrm{ABCD}$的内接四边形， $\angle \mathrm{BEG}$与 $\angle \mathrm{CFH}$都是锐角，已知 $\mathrm{EG}=3\mathrm{，}\mathrm{FH}=4$，四边形 $\mathrm{EFGH}$的面积为 $5$.求正方形 $\mathrm{ABCD}$的面积.

如图，四边形 $\mathrm{PQMN}$是 $\mathrm{}\mathrm{ABCD}$的内接四边形。

（1）若 $\mathrm{MP}//\mathrm{BC}$或 $\mathrm{NQ}//\mathrm{AB}$，求证 ${\mathrm{S}}_{\text{四边形}\text{PQMN}}=\frac{1}{2}{\mathrm{S}}_{\mathrm{◻ABCD}}$;

（2）若 ${\mathrm{S}}_{\text{四边形}\mathrm{PQMN}}=\frac{1}{2}{\mathrm{S}}_{\mathrm{◻ABCD}}$，问是否能推出 $\mathrm{MP}//\mathrm{BC}$或 $\mathrm{QN}//\mathrm{AB}$？证明你的结论.

如图，已知 $△\mathrm{BOF}\mathrm{，}△\mathrm{BOD}\mathrm{，}△\mathrm{AOF}\mathrm{，}△\mathrm{COE}$的面积分别为 $30$， $35$， $40$， $84$，求 ${\mathrm{S}}_{△\mathrm{ABC}}$.

如图是甲、乙在一次射击比赛中击中靶的情况（击中靶中心的圆面为 $10$环，靶中各数字表示该数所在圆环被击中所得的环数），每人射击了 $6$次.

（1）请用列表法将他俩射击的成绩统计出来；

（2）请你用学过的统计知识，对他们的 $6$次射击情况进行比较.

华中师大一附中理科实验班举行投篮比赛，下表显示了比赛的结果，上行的值表示投篮中的个数，下行的值表示投中 $\mathrm{n}$个球的参赛人数.

对比赛的结果还知道如下情况：

（1）获胜者投中 $15$个球；

（2）对投中 $3$个球或 $3$个以上球的参赛者来说，每人平均投中 $6$个球；

（3）对投中 $12$个球或 $12$个以下球的所有参赛者来说，每人平均投中 $5$个球；

问本次比赛所有参赛者投中的球的总数是多少?

如图所示的八个点处各写一个数字，已知每个点处所写的数字等于和这个点有线段相连的三个点处的数字的平均数，则代数式 $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}-\frac{1}{2}\mathrm{（}\mathrm{e}+\mathrm{f}+\mathrm{g}+\mathrm{h}\mathrm{）}}{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}-\frac{1}{3}\mathrm{（}\mathrm{e}+\mathrm{f}+\mathrm{g}+\mathrm{h}\mathrm{）}}$的值是多少?

某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分满分均为 $100$分，前六名选手的得分如下：

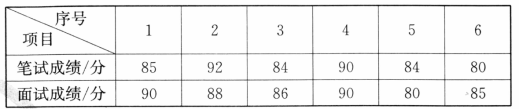
根据规定，笔试成绩和面试成绩分别按一定的百分比折合成绩（综合成绩的满分仍为 $100$分）.

（1）这 $6$名选手笔试成绩的中位数是＿＿＿＿＿分，众数是＿＿＿＿＿分；

（2）现得知 $1$号选手的综合成绩为 $88$分，求笔试成绩和面试成绩各占的百分比；

（3）求出其余 $5$名选手的综合成绩，并以综合成绩排序确定前两名人选.

某班参加一次智力竞赛，共 $\mathrm{a}\mathrm{，}\mathrm{b}\mathrm{，}\mathrm{c}$三道题，每题或者得满分或者得 $0$分，其中题 $\mathrm{a}$满分 $20\mathrm{，}\mathrm{b}\mathrm{，}\mathrm{c}$题满分分别为 $25$分，竞赛结果，每个学生至少答对了一题，三题全答对的有 $1$人，答对其中两道题的有 $15$人，答对题 $\mathrm{a}$的人数与答对题 $\mathrm{b}$的人数之和为 $29$；答对题 $\mathrm{a}$的人数与答对题 $\mathrm{c}$的人数之和为 $25$；答对题 $\mathrm{b}$的人数与答对题 $\mathrm{c}$的人数之和为 $20$，问这个班的平均成绩是多少?

阅读下面的材料，再回答问题：

一般地，如果函数 $\mathrm{y}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$对于自变量取值范围内的任意数 $\mathrm{x}$，都有 $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=-\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$，那么 $\mathrm{y}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$就叫做奇函数；如果函数 $\mathrm{y}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$对于自变量取值范围内的任意数 $\mathrm{x}$，都有 $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$，那么 $\mathrm{y}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$就叫做偶函数.

例如: $\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}={\mathrm{x}}^3+\mathrm{x}$.

当 $\mathrm{x}$取任意实数时， $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=\mathrm{（}-\mathrm{x}{\mathrm{）}}^3+\mathrm{（}-\mathrm{x}\mathrm{）}=-{\mathrm{x}}^3-\mathrm{x}=-\left({\mathrm{x}}^3+\mathrm{x}\right)$，即 $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=-\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$，所以 $\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}={\mathrm{x}}^3+\mathrm{x}$为奇函数.又如 $\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}=\left|\mathrm{x}\right|$，当 $\mathrm{x}$取任意实数时， $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=|-\mathrm{x}|=\left|\mathrm{x}\right|=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$，即 $\mathrm{f}\mathrm{（}-\mathrm{x}\mathrm{）}=\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}$，所以 $\mathrm{f}\mathrm{（}\mathrm{x}\mathrm{）}=\left|\mathrm{x}\right|$是偶函数.

问题（1）：下列函数中：① $\mathrm{y}={\mathrm{x}}^4$；② $\mathrm{y}={\mathrm{x}}^2+1$；③ $\mathrm{y}=\frac{1}{{\mathrm{x}}^3}$；④ $\mathrm{y}=\sqrt{\mathrm{x}+1}$；⑤ $\mathrm{y}=\mathrm{x}+\frac{1}{\mathrm{x}}$；所有奇函数是＿＿＿＿＿，所有偶函数是＿＿＿＿＿（只填序号）

问题（2）：请你再分别写出一个奇函数和一个偶函数.

某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按 $120$个工时计算）生产空调器、彩电、冰箱共 $360$台，且冰箱至少生产 $60$台，已知生产这些家电产品所需工时和每台产值如下表：

问：每周生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少（单位：千元）？