为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道 由西向东行驶.在 处测得岸边一建筑物 在北偏东 方向上,继续行驶40秒到达 处时,测得建筑物 在北偏西 方向上,如图所示,求建筑物 到赛道 的距离(结果保留根号).

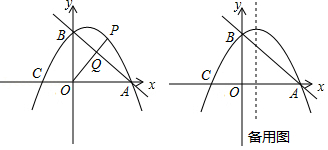
如图,直线 与 轴交于点 ,与 轴交于点 .抛物线 经过 、 两点,与 轴的另一个交点为 .
(1)求抛物线的解析式;
(2)点 是第一象限抛物线上的点,连接 交直线 于点 .设点 的横坐标为 , 与 的比值为 ,求 与 的函数关系式,并求出 与 的比值的最大值;
(3)点 是抛物线对称轴上的一动点,连接 、 ,设 外接圆的圆心为 ,当 的值最大时,求点 的坐标.
为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 |
乙种客车 |
|
载客量 (人 辆) |
30 |
42 |
租金 (元 辆) |
300 |
400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
如图,在平面直角坐标系中,矩形 的顶点 的坐标为 ,直线 与边 , 分别相交于点 , ,函数 的图象过点 .
(1)试说明点 也在函数 的图象上;
(2)将直线 沿 轴的负方向平移得到直线 ,当直线 与函数 的图象仅有一个交点时,求直线 的解析式.

近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 |
0 |
1 |
2 |
3 |
4 |
5 |
人数 |
11 |
15 |
23 |
28 |
18 |
5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
抛物线 与 轴交于点 , (点 在点 的左侧),与 轴交于点 ,其顶点为 .将抛物线位于直线 上方的部分沿直线 向下翻折,抛物线剩余部分与翻折后所得图形组成一个“ ”形的新图象.
(1)点 , , 的坐标分别为 , , ;
(2)如图①,抛物线翻折后,点 落在点 处.当点 在 内(含边界)时,求 的取值范围;
(3)如图②,当 时,若 是“ ”形新图象上一动点,是否存在以 为直径的圆与 轴相切于点 ?若存在,求出点 的坐标;若不存在,请说明理由.

问题:如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转 得到 ,连接 ,则线段 , , 之间满足的等量关系式为 ;
探索:如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论;
应用:如图③,在四边形 中, .若 , ,求 的长.

绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段 、折线 分别表示该有机产品每千克的销售价 (元)、生产成本 (元)与产量 之间的函数关系.
(1)求该产品销售价 (元)与产量 之间的函数关系式;
(2)直接写出生产成本 (元)与产量 之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?

如图,在平面直角坐标系中,直线 与反比例函数 在第二象限内的图象相交于点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移后与反比例函数图象在第二象限内交于点 ,与 轴交于点 ,且 的面积为 ,求直线 的解析式.

已知关于 的一元二次方程 .
(1)若该方程有两个实数根,求 的最小整数值;
(2)若方程的两个实数根为 , ,且 ,求 的值.
在2018年“新技术支持未来教育”的教师培训活动中,会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流,记者随机采访了部分参会教师,对他们发言的次数进行了统计,并绘制了不完整的统计表和条形统计图.
组别 |
发言次数 |
百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请你根据所给的相关信息,解答下列问题:
(1)本次共随机采访了 名教师, ;
(2)补全条形统计图;
(3)已知受访的教师中, 组只有2名女教师, 组恰有1名男教师,现要从 组、 组中分别选派1名教师写总结报告,请用列表法或画树状图的方法,求所选派的两名教师恰好是1男1女的概率.
