有 个命题:①一组对边相等,一组对角相等的四边形是平行四边形;②一组对边平行,一组对角相等的四边形是平行四边形;③ 是四边形 内一点,若 ,则四边形 是矩形;④若四边形的两条对角线互相垂直,则这个四边形是菱形.其中正确的命题个数是( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, 分别平分 和 ,直线 分别交 于点 .若 ,且 ,则 的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,矩形 的对角线交于 , 平分 交 于点 ,若 ,则 ( )
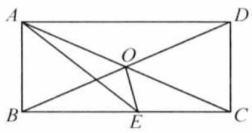
| A. |
|
B. |
|
C. |
|
D. |
|
平面上的一组 条平行线与另一组 条平行线相交,可构成平行四边形的个数为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知四边形 ,从下列条件中:① ⑤ ;⑥ .任取其中两个,可以得出“四边形 是平行四边形”这一结论的情况有( )
| A. | 种 |
B. | 种 |
C. | 种 |
D. | 种 |
如图,点 在平行四边形的对角线上,试判断 之间的大小关系( )

| A. |
|
B. |
|
C. |
|
D. | 无法确定 |
如图,长方形 的面积为 .对角线交于点 ,以 为邻边作平行四边形 ,对角线交于点 ;以 为邻边作平行四边形 ,以此类推,则 的面积为( )
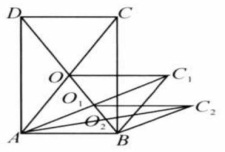
| A. |
|
B. |
|
C. |
|
D. |
|
给出下列命题:①一组对边和一组对角分别相等的四边形是平行四边形;②两组对角的内角平分线分别平行的四边形是平行四边形;③一组对边中点间的距离等于另一组对边边长和的一半的四边形是平行四边形;④两条对角线都平分四边形面积的四边形是平行四边形.其中,真命题有( )
| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
如图,在平行四边形 中, ,对角线 , 相交于点 ,则 的取值范围是( )

| A. |
|
B. |
|
C. |
|
D. |
|
四条线段的长分别为 (其中 为正实数),用它们拼成两个直角三角形,且 与 是其中的两条线段(如图),则 可取值的个数为( )

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
如图,设 满足下面条件: 是 上一点,且 ,而 长是整数且 .在所有这类三角形中最小的 的值是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形 的边长分别是 ,则最大正方形 的面积是( )

| A. |
|
B. |
|
C. |
|
D. |
|
某住宅小区有一块草坪如图所示,已知 , ,且 ,则这块草坪的面积是( )

| A. |
|
B. |
|
C. |
|
D. |
|
设一直角三角形的两条直角边为 ,斜边为 ,斜边上的高为 ,那么以 为边构成的三角形的形状是( )
| A. | 直角三角形 |
B. | 锐角三角形 |
| C. | 钝角三角形 |
D. | 不能确定,形状与 大小有关 |