在直角坐标系中,横、纵坐标都是整数的点称为整点,设 为整数,当直线 与 的交点为整点时, 的值可以取( )个.
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则一次函数 的图象必须经过的象限是( )
| A. | 第一、二象限 |
B. | 第一、二、三象限 |
| C. | 第二、三、四象限 |
D. | 第三、四象限 |
一条直线 ,其中 , 那么应该直线经过( )
| A. | 第二、四象限 |
B. | 第一、二、三象限 |
| C. | 第一、三象限 |
D. | 第二、三、四象限 |
已知如图a,点 是 中点,点 在 上,动点 以每秒 的速度沿图a的边线运动,运动路径为 ,相应的 的面积 关于运动的时间 图像如图b,若 ,则下列四个结论中正确的个数有( )
①图 中的 长是 ;②图b中的 点表示第 时 的值为 ;
③图a中的 长是 ;④图b中的 点表示第 时, 的值为 .

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
如图,某天,学校研究性学习小组的同学从 时起骑自行车外出调查, 时回学校,小组离开学校的距离与时间的关系可用图中的曲线表示,根据这个曲线图,下列说法错误的是( )

| A. | 在离校最远的地方调查的时间是 时 |
| B. | 第一次调查 时开始,历时 |
| C. | 中午 时休息的地方离校 |
| D. | 返校的速度最慢 |
“龟兔赛跑”讲述了这样的故事:龟兔同时出发,沿直线向同一目标奔跑,领先的兔子看着缓慢爬行的乌龟,骄傲起来,眯了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晩,乌龟还是先到达了终点….用 分别表示乌龟和兔子所行的路程, 为时间,则下列各图象与故事情节相吻合的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,一个粒子在第一象限内及 轴上运动,在第一分钟内它从原点运动到 ,而后它接着按图所示在 轴, 轴平行的方向来回运动且每分钟移动 个单位长度,那么在 分钟这一时刻,这个粒子所处的位置是( )
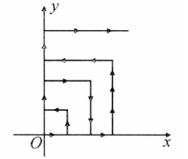
| A. |
|
B. |
|
C. |
|
D. |
|
如图是某函数的图象,则下列结论中正确的是( )

| A. | 当 时, 的取值是 |
B. | 当 时, 的取值是 |
| C. | 当 时,函数值 最大 |
D. | 当 时, 随 的增大而增大 |
如图所示的图象分别给出了 与 的对应关系,其中 是 的函数的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在梯形 中, 分别为 的中点,则 等于( )
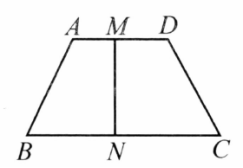
| A. |
|
B. |
|
C. |
|
D. |
|
如图四边形 是矩形, ,以对角线 为对称轴将 沿 对折则 点转移到 处, 与 交于 ,则 的面积为( )
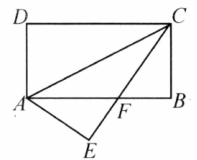
| A. |
|
B. |
|
C. |
|
D. |
|
已知三角形的三边长分别为 (其中 ),则此三角形( )
| A. | 一定是等边三角形 |
B. | 一定是等腰三角形 |
| C. | 一定是直角三角形 |
D. | 形状无法确定 |
若 是实数,且 ,则 的值是( )
| A. | 或 |
B. | 或 |
C. | 或 |
D. | 或 |