初中数学有理数无理数的概念与运算解答题

计算：．

先观察以下各式
，，…… （），根据以上规律计算：

 

利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？

如图，一个边长为1的正方形，依次取正方形的根据图示我们可以知道：第一次取走后还剩，即=1－；前两次取走+后还剩，即+=1－；前三次取走++后还剩，即++=1－；……前n次取走后，还剩       ，
即                      =         ．
利用上述计算：
(1) =            ．
(2) =           ．
(3) 2－2²－2³－2⁴－2⁵－2⁶－…－2²⁰¹¹+2²⁰¹²（本题写出解题过程）

有依次排列的3个数：3，9，8，对任相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，，，9，8，继续依次操作下去，问：从数串3，9，8开始操作第一百次以后所产生的那个新数串的所有数之和是多少？

计算：

利用4×4方格，作出面积为10cm²的正方形，然后在数轴上表示实数与－

（本小题共4分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少？
（3）从中取出2张卡片，使这2张卡片上数字组成一个最大的数，如何抽取？最大的数是多少？（4）从中取出4张卡片，用学过的运算方法，使结果为24．如何抽取？写出运算式子．（写出一种即可）．

如图，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是－2。

已知点A是数轴上的点，完成下列各题：
如果点A表示的数是3，将点A先向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
如果点A表示的数是－4，将点A先向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
一般地，如果点A表示的数是m，将点A先向右移动n个单位长度，再向左移动t个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________。

探索规律：观察下面由※组成的图案和算式，并解答问题




（）试猜想        ；
（）试猜想=            ；
（）请用上述规律计算：
 （请算出最后数值哦！）

某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在A处，规定向北方向为正，当天行驶纪录如下（单位：千米）
＋10，－9，＋7，－15，＋6，－14，＋4，－2
（1）A在岗亭何方？距岗亭多远？
（2）若摩托车行驶1千米耗油0.05升，这一天共耗油多少升？

将1，2，3……100，这100个自然数任意分成50组，每组两个数，将其中一个数记为a，另一个数记为b，代入代数式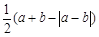中计算，求出其结果，50组都代入后可得50个值，求这50个值的和的最小值（请简要说明理由）．

图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为

　　　　　　
如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,，则最底层最左边这个圆圈中的数是               ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，，求图4中所有圆圈中各数的绝对值之和．

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为1²+2²+3²+…+n²．但n为100时，应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=n(n+1)(n—1)时，我们可以这样做：
(1)观察并猜想：
1²+2²=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
1²+2²+3²=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
1²+2²+3²+4²=(1+0)×1+(1+1)×2+(1+2)×3+               
=1+0×1+2+1×2+3+2×3+                        
=(1+2+3+4)+(                                  )
……
(2)归纳结论：
1²+2²+3²+…+n²=(1+0)×1+(1+1)×2+(1+2)×3+…+n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=(                      ) +
=                      +                                 
=×                     
(3)实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是              ．

观察下面的变形规律：
 ＝1－； ＝－；＝－；……
解答下面的问题：
（1）若n为正整数，请你猜想＝                  ；
（2）证明你猜想的结论；
（3）求和：＋＋＋…＋ .

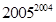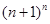（1）问题：你能比较和的大小吗？为了解决这个问题，首先写出它的一般形式，即比较和的大小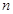（是正整数），然后我们从分析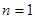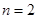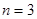，，，…这些简单情况入手，从中发现规律，经过归纳，猜想出结论.
通过计算，比较下列各组数的大小（在横线上填写“＞”、“＜”、“＝”号）：
，，，，，…
（2）从第（1）题的结果经过归纳，可以猜想出和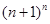的大小关系是什么？
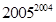（3）根据上面的归纳猜想，尝试比较和的大小.