已知在 中, 是 的中点, 是 延长线上的一点,连结 , .

(1)如图1,若 , , , ,求 的长.
(2)过点 作 ,交 延长线于点 ,如图2所示,若 , ,求证: .
(3)如图3,若 ,是否存在实数 ,当 时, ?若存在,请写出 的值;若不存在,请说明理由.
如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,在四边形 中, ,点 在 上, , ,垂足为 .
(1)求证:四边形 是平行四边形;
(2)若 平分 , , ,求 和 的长.
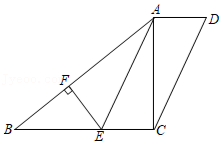
如图, 和
和 都是以A为直角顶点的等腰直角三角形,连结BD,BE,CE,延长CE交AB于点F,交BD于点G.
都是以A为直角顶点的等腰直角三角形,连结BD,BE,CE,延长CE交AB于点F,交BD于点G.
(1)求证: ;
;
(2)若 是边长可变化的等腰直角三角形,并将
是边长可变化的等腰直角三角形,并将 绕点
绕点 旋转,使CE的延长线始终与线段BD(包括端点B、D)相交.当
旋转,使CE的延长线始终与线段BD(包括端点B、D)相交.当 为等腰直角三角形时,求出
为等腰直角三角形时,求出 的值.
的值.
如图1为两个边长为1的正方形组成的 格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= ,如果是n个边长为1的正方形组成的
格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= ,如果是n个边长为1的正方形组成的 格点图,如图2,那么tan∠BPD= .
格点图,如图2,那么tan∠BPD= .
△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.

在 中, , 平分 ,交对角线 于点 ,交射线 于点 ,将线段 绕点 顺时针旋转 得线段 .
(1)如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;
(2)如图2,当 时,过点 作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 时,连接 ,若 ,请直接写出 与 面积的比值.

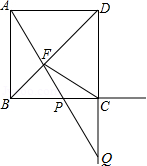
如图,正方形 的边长为1,点 在射线 上(异于点 、 ,直线 与对角线 及射线 分别交于点 、
(1)若 ,求 的度数;
(2)若点 在线段 上,过点 作 ,垂足为 ,当 时,求 的长;
(3)以 为直径作 .
①判断 和 的位置关系,并说明理由;
②当直线 与 相切时,直接写出 的长.
如图,△ABC中,AB=5,BC=11,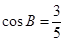 ,点P是BC边上的一个动点,联结AP,取AP的中点M,将线段MP绕点P顺时针旋转90°得到线段PN,联结AN,NC.
,点P是BC边上的一个动点,联结AP,取AP的中点M,将线段MP绕点P顺时针旋转90°得到线段PN,联结AN,NC.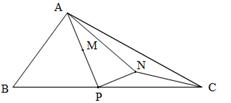
(1)当点N恰好落在BC边上时,求NC的长;
(2)若点N在△ABC内部(不含边界),设BP=x,CN=y,求y关于x的函数关系式,并求出函数的定义域;
(3)若△PNC是等腰三角形,求BP的长.
如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.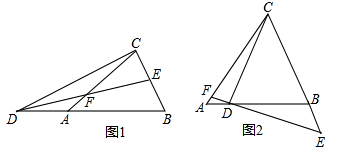
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).
公园中有一棵树和一座塔恰好座落在一条笔直的道路上.在途中A处,小杰测得树顶和塔尖的仰角分别为45º和30º,继续前进8米至B处,又测得树顶和塔尖的仰角分别为16º和45º,试问这棵树和这座塔的高度分别为多少米?(结果精确0.1米.参考数据: ≈1.414,
≈1.414, ≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961)
≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961)

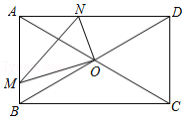
如图,在矩形 中, ,对角线相交于点 ,动点 从点 向点 运动(到点 即停止),点 是 上一动点,且满足 ,连结 .在点 、 运动过程中,则以下结论正确的是 .(写出所有正确结论的序号)
①点 、 的运动速度不相等;
②存在某一时刻使 ;
③ 逐渐减小;
④ .
如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为 .
.
(1)求小山的高度;
(2)求铁架的高度.
小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.