初中数学解直角三角形解答题

在 $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}$ ， $\angle \mathit{BAC}=\alpha$ ，点 $P$ 为线段 $\mathit{CA}$ 延长线上一动点，连接 $\mathit{PB}$ ，将线段 $\mathit{PB}$ 绕点 $P$ 逆时针旋转，旋转角为 $\alpha$ ，得到线段 $\mathit{PD}$ ，连接 $\mathit{DB}$ ， $\mathit{DC}$ ．

（1）如图1，当 $\alpha =60°$ 时，

①求证： $\mathit{PA}=\mathit{DC}$ ；

②求 $\angle \mathit{DCP}$ 的度数；

（2）如图2，当 $\alpha =120°$ 时，请直接写出 $\mathit{PA}$ 和 $\mathit{DC}$ 的数量关系．

（3）当 $\alpha =120°$ 时，若 $\mathit{AB}=6$ ， $\mathit{BP}=\sqrt{31}$ ，请直接写出点 $D$ 到 $\mathit{CP}$ 的距离为 　　．

如图，伞不论张开还是收紧，伞柄AP始终平分同一平面内两条伞架所成的角∠BAC，当伞收紧时，结点D与点M重合，且点A、E、D在同一条直线上，已知部分伞架的长度如下：单位：cm

伞架	DE	DF	AE	AF	AB	AC
长度	36	36	36	36	86	86

（1）求AM的长．
（2）当∠BAC=104°时，求AD的长（精确到1cm）．
备用数据：sin52°=0.788，cos52°=0.6157，tan52°=1.2799．

如图，菱形 $\mathit{ABCD}$ 的对角线 $\mathit{AC}$ 与 $\mathit{BD}$ 交于点 $O$ ， $\angle \mathit{ABC}:\angle \mathit{BAD}=1:2$ ， $\mathit{BE}//\mathit{AC}$ ， $\mathit{CE}//\mathit{BD}$ ．

（1）求 $\tan \angle \mathit{DBC}$ 的值；

（2）求证：四边形 $\mathit{OBEC}$ 是矩形．

如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP=74°，∠BEQ=30°；在点F处测得∠AFP=60°，∠BFQ=60°，EF=1km．

（1）判断AB，AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）．
（参考数据：≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）

如图，正方形 $\mathit{ABCD}$ 和正方形 $\mathit{CEFG}$ （其中 $\mathit{BD}>2\mathit{CE})$ ， $\mathit{BG}$ 的延长线与直线 $\mathit{DE}$ 交于点 $H$ ．

（1）如图1，当点 $G$ 在 $\mathit{CD}$ 上时，求证： $\mathit{BG}=\mathit{DE}$ ， $\mathit{BG}\perp \mathit{DE}$ ；

（2）将正方形 $\mathit{CEFG}$ 绕点 $C$ 旋转一周．

①如图2，当点 $E$ 在直线 $\mathit{CD}$ 右侧时，求证： $\mathit{BH}-\mathit{DH}=\sqrt{2}\mathit{CH}$ ；

②当 $\angle \mathit{DEC}=45°$ 时，若 $\mathit{AB}=3$ ， $\mathit{CE}=1$ ，请直接写出线段 $\mathit{DH}$ 的长．

已知△ABC中的∠A与∠B满足（1-tanA）²+|sinB-|=0
（1）试判断△ABC的形状．
（2）求（1+sinA）²-2-（3+tanC）⁰的值．

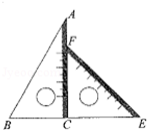
数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含 $45°$的三角板的斜边与含 $30°$的三角板的长直角边相等，于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点 $B$， $C$， $E$在同一直线上，若 $\mathit{BC}=2$，求 $\mathit{AF}$的长．

请你运用所学的数学知识解决这个问题．

如图，在 $▱\mathit{ABCD}$ 中， $E$ ， $F$ 是对角线 $\mathit{BD}$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $\angle \mathit{AEB}=\angle \mathit{CFD}=90°$ ．

（1）求证：四边形 $\mathit{AECF}$ 是平行四边形；

（2）当 $\mathit{AB}=5$ ， $\tan \angle \mathit{ABE}=\frac{3}{4}$ ， $\angle \mathit{CBE}=\angle \mathit{EAF}$ 时，求 $\mathit{BD}$ 的长．

如图，已知 $\mathit{AB}$ 是 $\odot O$ 的直径， $\angle \mathit{ACD}$ 是 $\widehat{\mathit{AD}}$ 所对的圆周角， $\angle \mathit{ACD}=30°$ ．

（1）求 $\angle \mathit{DAB}$ 的度数；

（2）过点 $D$ 作 $\mathit{DE}\perp \mathit{AB}$ ，垂足为 $E$ ， $\mathit{DE}$ 的延长线交 $\odot O$ 于点 $F$ ．若 $\mathit{AB}=4$ ，求 $\mathit{DF}$ 的长．

如图，已知点 $C$ 是以 $\mathit{AB}$ 为直径的半圆上一点， $D$ 是 $\mathit{AB}$ 延长线上一点，过点 $D$ 作 $\mathit{BD}$ 的垂线交 $\mathit{AC}$ 的延长线于点 $E$ ，连结 $\mathit{CD}$ ，且 $\mathit{CD}=\mathit{ED}$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）若 $\tan \angle \mathit{DCE}=2$ ， $\mathit{BD}=1$ ，求 $\odot O$ 的半径．

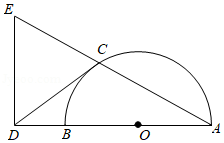
数学小组研究如下问题：长春市的纬度约为北纬 $44°$ ，求北纬 $44°$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：

（1）在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

（2）如图， $\odot O$ 是经过南、北极的圆，地球半径 $\mathit{OA}$ 约为 $6400\mathit{km}$ ．弦 $\mathit{BC}//\mathit{OA}$ ，过点 $O$ 作 $\mathit{OK}\perp \mathit{BC}$ 于点 $K$ ，连接 $\mathit{OB}$ ．若 $\angle \mathit{AOB}=44°$ ，则以 $\mathit{BK}$ 为半径的圆的周长是北纬 $44°$ 纬线的长度；

（3）参考数据： $\pi$ 取3， $\sin 44°=0.69$ ， $\cos 44°=0.72$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\mathit{BC}//\mathit{OA}$ ， $\angle \mathit{AOB}=44°$ ，

所以 $\angle B=\angle \mathit{AOB}=44°($ 　　 $)$ （填推理依据），

因为 $\mathit{OK}\perp \mathit{BC}$ ，所以 $\angle \mathit{BKO}=90°$ ，

在 $\text{Rt}\Delta \text{BOK}$ 中， $\mathit{OB}=\mathit{OA}=6400$ ．

$\mathit{BK}=\mathit{OB}\times$ 　　（填" $\sin B$ "或" $\cos B$ " $)$ ．

所以北纬 $44°$ 的纬线长 $C=2\pi \cdot \mathit{BK}$ ．

$=2\times 3\times 6400\times$ 　　（填相应的三角形函数值）

$\approx$ 　　 $\left(\mathit{km}\right)$ （结果取整数）．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=m$， $\mathit{BC}=n$， $m>n$，点 $P$是边 $\mathit{AB}$上一点，连接 $\mathit{CP}$，将 $\mathit{\Delta ACP}$沿 $\mathit{CP}$翻折得到 $\mathit{\Delta QCP}$．

（1）若 $m=4$， $n=3$，且 $\mathit{PQ}\perp \mathit{AB}$，求 $\mathit{BP}$的长；

（2）连接 $\mathit{BQ}$，若四边形 $\mathit{BCPQ}$是平行四边形，求 $m$与 $n$之间的关系式．

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{BC}$，点 $O$是 $\mathit{AC}$的中点，点 $P$是 $\mathit{AC}$上的一个动点（点 $P$不与点 $A$， $O$， $C$重合）．过点 $A$，点 $C$作直线 $\mathit{BP}$的垂线，垂足分别为点 $E$和点 $F$，连接 $\mathit{OE}$， $\mathit{OF}$．

（1）如图1，请直接写出线段 $\mathit{OE}$与 $\mathit{OF}$的数量关系；

（2）如图2，当 $\angle \mathit{ABC}=90°$时，请判断线段 $\mathit{OE}$与 $\mathit{OF}$之间的数量关系和位置关系，并说明理由

（3）若 $|\mathit{CF}-\mathit{AE}|=2$， $\mathit{EF}=2\sqrt{3}$，当 $\mathit{\Delta POF}$为等腰三角形时，请直接写出线段 $\mathit{OP}$的长．

如图，抛物线 $y=a{x}^2+\mathit{bx}-5(a\ne 0)$ 经过点 $A(4,-5)$ ，与 $x$ 轴的负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $\mathit{OC}=5\mathit{OB}$ ，抛物线的顶点为点 $D$ ．

（1）求这条抛物线的表达式；

（2）联结 $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DA}$ ，求四边形 $\mathit{ABCD}$ 的面积；

（3）如果点 $E$ 在 $y$ 轴的正半轴上，且 $\angle \mathit{BEO}=\angle \mathit{ABC}$ ，求点 $E$ 的坐标．