如图,是
的直径,过
外一点
作
的两条切线
,
,切点分别为
,
,连接
,
.
(1)求证:;
(2)连接,
,若
,
,
,求
的长.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点O)的南偏东450方向的B点生成,测得 。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。

(1)台风中心生成点B的坐标为( ),台风中心转折点C的坐标为( );(结果保留根号)
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
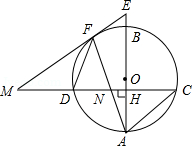
如图,已知 是圆 的直径,弦 ,垂足为 ,与 平行的圆 的一条切线交 的延长线于点 ,交 的延长线于点 ,切点为 ,连接 交 于点 .
(1)求证: ;
(2)连接 ,若 , ,求圆 的直径的长度.
如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).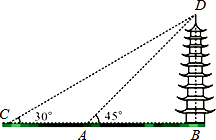
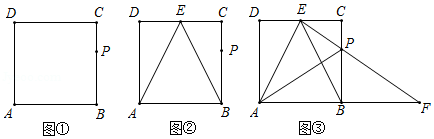
如图,在矩形 中, , , 是 边上的一点,且 .
(1)用尺规在图①中作出 边上的中点 ,连接 、 (保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断 是否平分 ,并说明理由;
(3)如图③,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 ,不添加辅助线, 能否由都经过 点的两次变换与 组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
如图所示,在矩形 中,点 在线段 上,点 在线段 的延长线上,连接 交线段 于点 ,连接 ,若 .
(1)求证:四边形 是平行四边形;
(2)若 ,求线段 的长度.

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,已知 是 的直径, 是 所对的圆周角, .
(1)求 的度数;
(2)过点 作 ,垂足为 , 的延长线交 于点 .若 ,求 的长.

如图,已知点 是以 为直径的半圆上一点, 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,连结 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
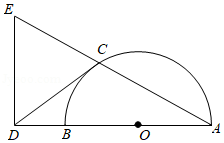
数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
(2)如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
(3)参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 (填推理依据),
因为 ,所以 ,
在 中, .
(填" "或" " .
所以北纬 的纬线长 .
(填相应的三角形函数值)
(结果取整数).

如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

如图1,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , , ,等边 的顶点 与原点 重合, 边落在 轴正半轴上,点 恰好落在线段 上,将等边 从图1的位置沿 轴正方向以每秒1个单位长度的速度平移,边 , 分别与线段 交于点 , (如图2所示),设 平移的时间为 .
(1)等边 的边长为 ;
(2)在运动过程中,当 时, 垂直平分 ;
(3)若在 开始平移的同时.点 从 的顶点 出发.以每秒2个单位长度的速度沿折线 运动.当点 运动到 时即停止运动. 也随之停止平移.
①当点 在线段 上运动时,若 与 相似.求 的值;
②当点 在线段 上运动时,设 ,求 与 的函数关系式,并求出 的最大值及此时点 的坐标.

在 中, ,点 是 的中点,点 是 上的一个动点(点 不与点 , , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 ,连接 , .
(1)如图1,请直接写出线段 与 的数量关系;
(2)如图2,当 时,请判断线段 与 之间的数量关系和位置关系,并说明理由
(3)若 , ,当 为等腰三角形时,请直接写出线段 的长.
