初中数学解直角三角形解答题

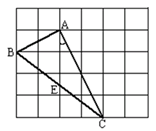
如图，两建筑物的水平距离BC为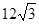米，从点A测得点D的俯角α＝30°，测得点C的俯角β＝60°，求建筑物CD的高度．

计算：．

计算：－sin30°
解方程：

某校初三课外活动小组，在测量树高的一次活动中．如图所示，测得树底部中心A到斜坡底C的水平距离为8.8m，在阳光下某一时刻测得l米的标杆影长为0.8m，树影落在斜坡上的部分CD=3.2m，已知斜坡CD的坡比，求树高AB．（结果保留整数，参考数据：≈1.7）．
                               

如图5，一架飞机在空中P处探测到某高山山顶D处的俯角为60°，
此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行，飞行10秒到山顶D的正上方C处，此时测得飞机距地平面的垂直高度为12千米，求这座山的高（精确到0.1千米）

计算：－(－4)+－2cos30°

计算：

两幢垂直于地面的大楼相距110米，从甲楼顶部看乙楼顶部的仰角为30°，已知甲楼高35米
根据题意，在图中画出示意图；
求乙楼的高度为多少米？

如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF＝3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

计算：
计算： 2 －tan60°+(－1)
解方程：

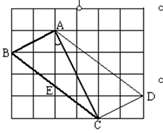
问题背景：在中，、、三边的长分别为、、，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图①所示．这样不需求的高，而借用网格就能计算出它的面积．
请你将的面积直接填写在横线上．_________________________思维拓展：
我们把上述求面积的方法叫做构图法．若 三边的长分别为、、（），请利用图②的正方形网格（每个小正方形的边长为）画出相应的，并求出它的面积．探索创新：
若三边的长分别为、、（，且），试运用构图法求出这三角形的面积．

两幢垂直于地面的大楼相距110米，从甲楼顶部看乙楼顶部的仰角为30°，已知甲楼高35米
根据题意，在图中画出示意图；
求乙楼的高度为多少米？

某校把一块沿河的三角形废地（如图）开辟为生物园，已知∠ACB＝90°，
∠CAB＝54°，BC＝60米．
现学校准备从点C处向河岸AB修一条小路CD，使得CD将生物园分割成面积相等的两部分．请你用直尺和圆规在图中作出小路CD（保留作图痕迹）；
为便于浇灌，学校在点C处建了一个蓄水池，利用管道从河中取水．已知每铺设1米管道费用为50元，求铺设管道的最低费用.（sin36°≈0.588，cos36°≈0.809，tan36°≈0.727，精确到1元）

如图，某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B处测得C地的仰角为60°，已知C地比A地高200m。求电缆BC的长（结果保留根号）.

如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：
用签字笔画AD∥BC（D为格点），连接CD.　
线段AB的长为_    ，△ABC的面积为_     .　
若E为BC中点，则tan∠CAE的值是_   .