如图,为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底B端8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树AB的高度约为( )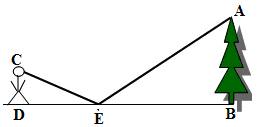
| A.4.2米 | B.4.8米 | C.6.4米 | D.16.8米 |
在Rt△ABC 中,∠C = 90°,∠A、∠B、与∠C的对边分别是a、b和c那么下列关系式中,正确的是( )
A.cosA=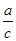 B.tanA=
B.tanA=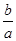 C.sinA=
C.sinA=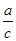 D.cosA=
D.cosA=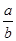
如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2 海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )
| A.2 海里 | B. 海里 海里 |
C. 海里 海里 |
D. 海里 海里 |
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A. |
B. |
C. |
D. |
如图,斜面AC的坡度(CD与AD的比)为1:2,AC= 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )
米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )
| A.5米 | B.6米 | C.8米 | D. 米 米 |
下列命题中,真命题的个数是( )
①若-1<x< - , 则-2<
, 则-2< <-1;
<-1;
②若-1≤x≤2,则1≤x2≤4;
③凸多边形的外角和为360°;
④三角形中,若∠A+∠B=90°,则sinA=cosB.
A.4 B.3 C.2 D.1
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= |
B.cosA= |
C.tanA= |
D.tanB= |
下列运算:sin30°= ,
, .其中运算结果正确的个数为( )
.其中运算结果正确的个数为( )
| A.4 | B.3 | C.2 | D.1 |
如图,在△ABC中,∠BAC=Rt∠,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
A. |
B. |
C. |
D. |
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE 沿AE折叠,点B落在点F处,连接FC,则sin∠ECF =( )
A. |
B. |
C. |
D. |
如图,△ABC中,∠B=90°,BC=2AB,则cosA=( )
A.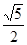 |
B.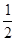 |
C. |
D. |
如图,D是等边△ABC边AD上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC、BC上,则CE:CF=( )

A、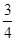 B、
B、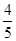 C、
C、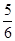 D、
D、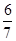
如图,要在宽为22米的九洲大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120º角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直。当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应设计为( )
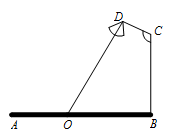
A.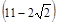 米 米 |
B.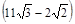 米 米 |
C. 米 米 |
D.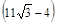 米 米 |
如图,△ABC中,∠B=60°,∠ACB=75°,点D是BC边上一动点,以AD为直径作⊙O,分别交AB、AC于E、F,若弦EF的最小值为1,则AB的长为( )
A. B.
B. C.1.5 D.
C.1.5 D.
如图,在△ABC中,∠C=Rt∠,AB=5,BC=3,则sinA的值是( )
A.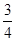 |
B. |
C.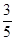 |
D.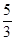 |