初中数学解直角三角形试题

如图，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外侧作Rt△ABE和Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q，

（1）若Rt△ABE和Rt△ACF都是等腰三角形，直接写出EP与FQ有怎样的数量关系；
（2）若Rt△ABE和Rt△ACF中满足AB=" k" AE，AC=" k" AF时，（1）中的结论还成立吗？若成立，请证明；若不成立，请探究EP与FQ有怎样的数量关系？
（3）若Rt△ABE和Rt△ACF中满足AB=" k" AE，AC= mAF时，联结EF交射线GA于点D，试探究ED与FD有怎样的数量关系？

在一次对某水库大坝设计中，李设计师对修建一座长80米的水库大坝提出了以下方案：大坝的横截面为等腰梯形，如图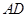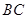，∥，坝高10m，迎水坡面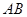的坡度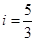，审核组专家看后，从力学的角度对此方案提出了建议，李设计师决定在原方案的基础上，将迎水坡面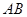的坡度进行修改，修改后的迎水坡面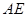的坡度．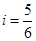

（1）求原方案中此大坝迎水坡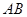的长（结果保留根号）
（2）如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿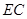方向拓宽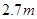，求坝底将会沿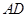方向加宽多少米？

在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线（线段AC）长20m，风筝B的引线（线段BC）长24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°.
（1）试通过计算，比较风筝A与风筝B谁离地面更高？
（2）求风筝A与风筝B的水平距离.(精确到0.01 m；参考数据：sin45°≈0.707,cos45°≈0.707,tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732）

如图，山坡上有一棵树AB，树底部B点到山脚C点的距离BC为米，山坡的坡角为30°．小宁在山脚的平地F处测量这棵树的高，点C到测角仪EF的水平距离CF=1米，从E处测得树顶部A的仰角为45°，树底部B的仰角为20°，求树AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5.
（Ⅰ)探究新知：
如图①⊙O是△ABC的内切圆，与三边分别相切于点E、F、G..
（1）求证内切圆的半径r₁="1;"
（2）求tan∠OAG的值；
（Ⅱ）结论应用
（1）如图②若半径为r₂的两个等圆⊙O₁、⊙O₂外切，且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂的值；
（2）如图③若半径为r_n的n个等圆⊙O₁、⊙O₂、…、⊙O_n依次外切，且⊙O₁与AC、AB相切，⊙O_n与BC、AB相切，⊙O₁、⊙O₂、…、⊙O_n均与AB相切，求r_n的值.

如图，2012年4月10日，中国渔民在中国南海黄岩岛附近捕鱼作业，中国海监船在A地侦查发现，在南偏东60°方向的B地，有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶，企图抓捕正在C地捕鱼的中国渔民，此时，C地位于中国海监船的南偏东45°方向的10海里处，中国海监船以每小时30海里的速度赶往C地救援我国渔民，能不能及时赶到？（≈1.41，≈1.73，=2.45）．

如图，一轮船在O处测得小岛A在北偏西60°的方向上，则∠AOB=30°轮船继续往正西航行100海里到达B处，测得此时∠OBA=135°，如果轮船继续往西航行，那么小岛A离轮船的最近距离是多少海里?（答案保留根号）

在云南大理坐落着美丽的大理三塔．数学活动小组开展课外实践活动，在一个阳光明媚的上午，他们去测量三塔中一塔的高度，携带的测量工具有：测角仪．皮尺．小镜子．
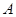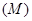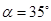（1）小华利用测角仪和皮尺测量塔高． 图1为小华测量塔高的示意图．她先在塔前的平地上选择一点，用测角仪测出看塔顶的仰角，在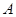点和塔之间选择一点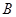，测出看塔顶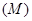的仰角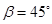，然后用皮尺量出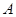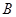．两点的距离为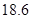m,自身的高度为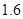m．请你利用上述数据帮助小华计算出塔的高度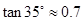（，结果保留整数）．

（2）如果你是活动小组的一员，正准备测量塔高，而此时塔影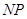的长为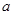m（如图2）,你能否利用这一数据设计一个测量方案？如果能，
请回答下列问题：
①在你设计的测量方案中，选用的测量工具是:                            ；
②要计算出塔的高，你还需要测量哪些数据？                                   ．

已知圆锥的底面半径为5cm，侧面积为cm²，设圆锥的母线与高的夹角为（如图 所示），则的值为（   ）

A．

B．

C．

D．

某时刻海上点P处有一客轮，测得灯塔A位于客轮P的北偏东30°方向，且相距20海里.客轮以60海里/小时的速度沿北偏听偏西60°方向航行小时到达B处，那么tan∠ABP=【   】

A．

B．2

C．

D．

丽水市在规划新城期间，欲拆除瓯江岸边的一根电线杆AB(如图)，已知距电线杆AB水平距离14米处是河岸，即BD＝14米，该河岸的坡面CD的坡角∠CDF的正切值为2（即tan∠CDF=2），岸高CF为2米，在坡顶C处测得杆顶A的仰角为30°，D、E之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB时，为确保安全，是否将此人行道封上？(在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域)

如图，我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃
跑，我缉私艇迅速朝A的西偏北60⁰的方向出水拦截，2小时后终于在B地正北方向M处拦截住，试求缉私
船的速度．（参考数据：）

如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA=100米，山坡坡度且O,A,B在同一条直线上．求电视塔OC的高度以及此人所在位置P的铅直高度PB．（测倾器高度忽略不计，结果保留根号形式）

小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD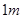＝，CE＝，CA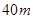＝（点A、E、C在同一直线上）．已知小明的身高EF是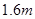，请你帮小明求出楼高AB．

如图1，在Rt△ABC中，∠C＝90°，AC＝9cm，BC＝12cm．在Rt△DEF中，∠DFE＝90°，EF＝6cm，
DF＝8cm．E，F两点在BC边上，DE，DF两边分别与AB边交于G，H两点．现固定△ABC不动，△DEF从点F
与点B重合的位置出发，沿BC以1cm/s的速度向点C运动，点P从点F出发，在折线FD—DE上以2cm/s的速
度向点E运动．△DEF与点P同时出发，当点E到达点C时，△DEF和点P同时停止运动．设运动的时间是
t（单位：s），t＞0．
（1）当t＝2时，PH=    cm ，DG =    cm；
（2）t为多少秒时△PDE为等腰三角形？请说明理由；
（3）t为多少秒时点P与点G重合？写出计算过程；
（4）求tan∠PBF的值（可用含t的代数式表示）．